题目内容
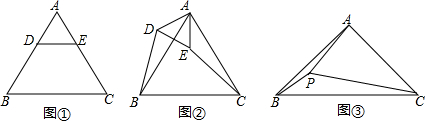
6.如图在△ABC中,D为BC上一点,且BD=2CD.(1)如图1,若∠BAC=90°,AB=AC=6,求AD;
(2)如图2,若∠BAC=105°,∠CAD=30°,求$\frac{AD}{AC}$的值;
(3)如图3,若∠BAC=120°,∠CAD=30°,点E在AD的延长线上,且∠ACE=75°,BE=2$\sqrt{6}$,求AD的长.
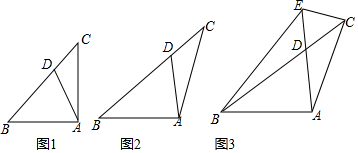
分析 (1)如图1中,作DM⊥AB于M.易知△BDM是等腰直角三角形,可得BM=DM,由DM∥AC,推出$\frac{BD}{BC}$=$\frac{DM}{AC}$=$\frac{2}{3}$,推出DM=4,推出BM=DM=4,AM=2,在Rt△ADM中,根据AD=$\sqrt{D{M}^{2}+A{M}^{2}}$计算即可解决问题.
(2)如图2中,作CM∥AD交BA的延长线于M.首先证明AC=CM,由AD∥CM,可得$\frac{AD}{CM}$=$\frac{BD}{BC}$=$\frac{2}{3}$,由此即可解决问题;
(3)作CM∥AD交BA的延长线于M.只要证明AC=AE=AB,求出AB,即可解决问题;
解答 解:(1)如图1中,作DM⊥AB于M.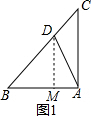
∵AB=AC,∠BAC=90°,
∴∠B=45°,
∴△BDM是等腰直角三角形,
∴BM=DM,
∵DM∥AC,
∴$\frac{BD}{BC}$=$\frac{DM}{AC}$=$\frac{2}{3}$,
∴DM=4,
∴BM=DM=4,AM=2,
在Rt△ADM中,AD=$\sqrt{D{M}^{2}+A{M}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
(2)如图2中,作CM∥AD交BA的延长线于M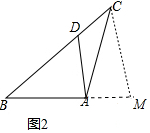
∵∠BAC=105°,∠DAC=30°,
∴∠BAD=75°,∠CAM=75°,
∵AD∥CM,
∴∠M=∠BAD=75°,
∴∠M=∠CAM,
∴AC=CM,
∵AD∥CM,
∴$\frac{AD}{CM}$=$\frac{BD}{BC}$=$\frac{2}{3}$,
∴$\frac{AD}{AC}$=$\frac{2}{3}$.
(3)作CM∥AD交BA的延长线于M.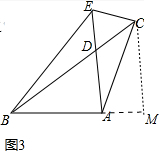
∵∠BAC=120°,∠DAC=30°,
∴∠BAD=∠M=90°,
∵∠ACE=75°,∠CAE=30°,
∴∠AEC=∠ACE=75°,
∴AC=AE,
在Rt△ACM中,设AM=a,则AC=2a,
∵AD∥CM,
∴AB:BM=BD:BC=2:3,
∴AB=2a=AC,
∴∠ABC=∠ACB,
∵∠BAC=120°,
∴∠ABD=30°,
在Rt△ABE中,AB=AE=$\frac{\sqrt{2}}{2}$BE=2$\sqrt{3}$,
在Rt△ABD中,AD=AB•tan30°=2.
点评 本题考查等腰三角形的判定和性质、平行线分线段成比例定理,锐角三角函数、等腰直角三角形的性质和判定等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案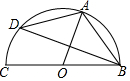 如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$且x≠0 | C. | x≥$\frac{1}{2}$ | D. | x>$\frac{1}{2}$且x≠0 |
| A. | 6,-6 | B. | 3,7 | C. | 0,6 | D. | 0,7 |