题目内容
14.已知,△ABC是等腰三角形,AB=AC.(1)当AD=AE,∠DAE=∠BAC时,
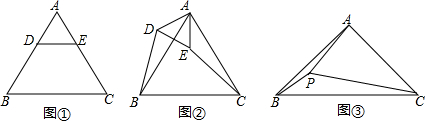
①特殊情形:如图①,若点D、E分别在边AB、AC上,则DB=EC.(填“>”、“<”或“=”).
②发现探究:如图②,若将图①中的△ADE绕点A旋转,当点D在△ABC外部,点E在△ABC内部时,①中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(2)拓展运用:如图③,点P在△ABC内部,∠BAC=90°,且PA=2,PB=1,PC=3,则∠APB的大小为135度.
分析 (1)①由DE∥BC,得到 $\frac{DB}{AB}$=$\frac{EC}{AC}$,结合AB=AC,得到DB=EC;②由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;
(2)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
解答 解:(1)①∵DE∥BC,
∴$\frac{DB}{AB}$=$\frac{EC}{AC}$,
∵AB=AC,
∴DB=EC,
故答案为:=,
②成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中
$\left\{\begin{array}{l}{AD=AE}\\{∠DAB=∠EAC}\\{AB=AC}\end{array}\right.$,
∴△DAB≌△EAC,
∴DB=CE,
(2)如图,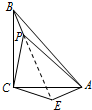
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2 $\sqrt{2}$,
在△PEA中,PE2=(2 $\sqrt{2}$)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°.
故答案为135°.
点评 此题是几何变换综合题,主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.

练习册系列答案
相关题目
5.一组数据8,3,8,6,7,8,7的众数和极差分别是( )
| A. | 8,3 | B. | 8,5 | C. | 7,8 | D. | 8,7 |
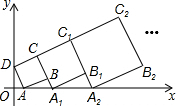 在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032.
在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为5×($\frac{3}{2}$)4032.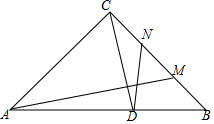 已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN
已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN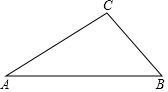 如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.
如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.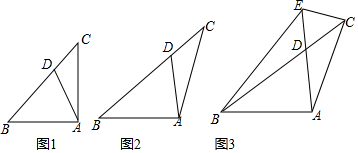
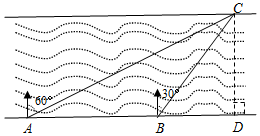 如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,
如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,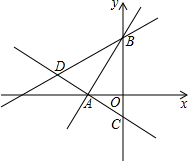 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根.
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根.