题目内容
11.(1)解分式方程:$\frac{1-x}{x-2}$+2=$\frac{1}{2-x}$;(2)求不等式组$\left\{\begin{array}{l}2x+5≤3(x+2)\\ \frac{x-1}{2}<\frac{x}{3}\end{array}$的解集.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解答 解:(1)去分母得:1-x+2x-4=-1,
解得:x=2,
经检验,x=2是原方程的增根,原方程无解;
(2)$\left\{\begin{array}{l}{2x+5≤3(x+2)①}\\{\frac{x-1}{2}<\frac{x}{3}②}\end{array}\right.$,
由①得:x≥-1,
由②得:x<3,
则不等式组的解集为:-1≤x<3.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.2016年海口市财政收入达25 000 000 000元,该数据用科学记数法表示为( )
| A. | 25×1010 | B. | 0.25×1012 | C. | 2.5×1010 | D. | 2.5×1011 |
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
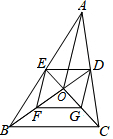 如图,在△ABC中,中线BD与CE相交于点O,F、G分别是BO、CO的中点,连接AO,若AO=6,四边形DEFG的周长为14,则BC=( )
如图,在△ABC中,中线BD与CE相交于点O,F、G分别是BO、CO的中点,连接AO,若AO=6,四边形DEFG的周长为14,则BC=( )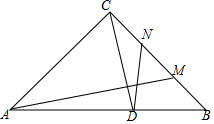 已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN
已知△ABC中,AC=BC,∠CAB=∠CBA=45°,点M为直线BC上任意一点,过点C作CD⊥AM交AB于点D,在BC上取一点N使CN=BM,连接DN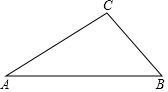 如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.
如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.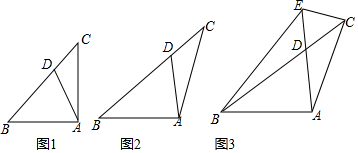
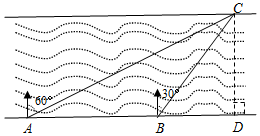 如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,
如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,


