题目内容
19.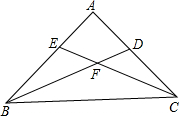 如图,在△ABC中,∠ABC、∠ACB的平分线相交于点F.
如图,在△ABC中,∠ABC、∠ACB的平分线相交于点F.(1)若∠ABC=40°,∠ACB=50°,求∠BFC的度数.
(2)若∠A=70°,求∠BFC的度数;
(3)若∠BFC=120°,求∠A的度数;
(4)根据上述信息,试探究∠A与∠BFC之间的关系,并说明理由.
分析 (1)根据角平分线的定义可得∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,再根据三角形内角和定理求出即可;
(2)根据三角形内角和定理求出∠ABC+∠ACB,根据角平分线定义求出∠FBC+∠FCB,根据三角形内角和定理求出即可;
(3)根据三角形内角和定理求出∠FBC+∠FCB,求出∠ABC+∠ACB,根据三角形内角和定理求出即可;
(4)根据角平分线的定义可得∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,然后表示出∠FBC+∠FCB,再根据三角形的内角和等于180°列式整理即可得证.
解答 解:(1)∵∠ABC、∠ACB的平分线相交于点F,∠ABC=40°,∠ACB=50°,
∴∠FBC=$\frac{1}{2}$∠ABC=20°,∠FCB=$\frac{1}{2}$∠ACB=25°,
∴∠BFC=180°-(∠FBC+∠FCB)=135°;
(2)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°,
∵∠ABC、∠ACB的平分线相交于点F,
∴∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠FBC+∠FCB=55°,
∴∠NFC=180°-(∠FBC+∠FCB)=62.5°;
(3)∵∠BFC=120°,
∴∠FBC+∠FCB=180°-∠BFC=60°,
∵∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠ABC+∠ACB=120°,
∴∠A=180°-(∠ABC+∠ACB)=60°;
(4)∠BFC=90°+$\frac{1}{2}∠$A,
理由是:∵∠ABC与∠ACB的平分线相交于点F,
∴∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠FBC+∠FCB=$\frac{1}{2}$(∠ABC+∠ACB),
在△FBC中,∠BFC=180°-(∠FBC+∠FCB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A.
点评 本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案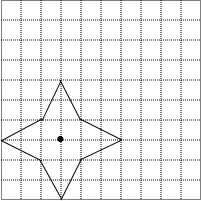 如图,一朵四瓣花飘动在10×10的网格中.
如图,一朵四瓣花飘动在10×10的网格中.