题目内容
10.在Rt△ABC中,BC=a,AC=b,CD使斜边AB上的高,则三个直角三角形(△ABC,△ACD,△BCD)的内切圆半径的和等于$\frac{{ab\sqrt{{a^2}+{b^2}}}}{{{a^2}+{b^2}}}$.分析 在Rt△ABC中根据勾股定理得到AB=$\sqrt{{a}^{2}+{b}^{2}}$,由CD是斜边AB上的高,根据三角形的面积公式得到CD=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$,根据射影定理得到AC2=AD•AB,BC2=BD•AB,AD=$\frac{{b}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}$,BD=$\frac{{a}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}$,然后根据三角形内切圆的半径=$\frac{a+b-c}{2}$,即可得到结果.
解答 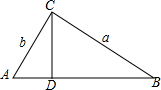 解:如图,在Rt△ABC中,∵BC=a,AC=b,
解:如图,在Rt△ABC中,∵BC=a,AC=b,
∴AB=$\sqrt{{a}^{2}+{b}^{2}}$,
∵CD是斜边AB上的高,
∴CD=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$,
∵∠ACB=∠CDA=∠CDB=90°,
∴△ACD∽△BCD∽△ABC,
∴AC2=AD•AB,BC2=BD•AB,
∴AD=$\frac{{b}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}$,BD=$\frac{{a}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}$,
设直角三角形△ABC,△ACD,△BCD的内切圆半径分别为:r1,r2,r3,
∴r1+r2+r3=$\frac{a+b-\sqrt{{a}^{2}+{b}^{2}}}{2}$+$\frac{\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}+\frac{{b}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}-b}{2}$+$\frac{\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}+\frac{{a}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}-a}{2}$=$\frac{2ab}{2\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab\sqrt{{a}_{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}$.
故答案为:$\frac{{ab\sqrt{{a^2}+{b^2}}}}{{{a^2}+{b^2}}}$.
点评 本题考查了三角形的内切圆和内心,直角三角形的性质,射影定理,熟练掌握直角三角形的内切圆的半径=$\frac{a+b-c}{2}$是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{1001}{2004}$ | B. | $\frac{1001}{1002}$ | C. | $\frac{2004}{2005}$ | D. | $\frac{1002}{2005}$ |
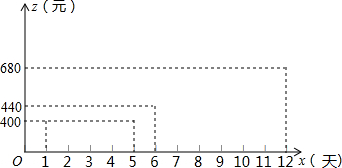 在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走.为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高.这样每天生产的服装数量y(套)与时间x(元)的关系如表:
在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走.为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高.这样每天生产的服装数量y(套)与时间x(元)的关系如表:| 时间x(天) | 1 | 2 | 3 | 4 | … |
| 每天产量y(套) | 22 | 24 | 26 | 28 | … |
(1)判断每天生产的服装的数量y(套)与生产时间x(元)之间是我们学过的哪种函数关系?并验证.
(2)已知这批外贸服装的订购价格为每套1570元,设车间每天的利润为w(元).求w(元)与x(天)之间的函数关系式,并求出哪一天该生产车间获得最高利润,最高利润是多少元?
(3)从第6天起,该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金,但必须保证每天扣除捐款后的利润随时间的增大而增大.求a的最大值,此时留守儿童共得多少元基金?
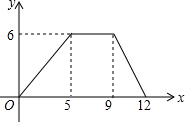 如图,是一对变量满足的函数关系的图象.有下列3个不同的问题情境:
如图,是一对变量满足的函数关系的图象.有下列3个不同的问题情境: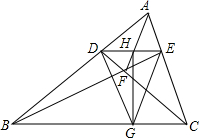 在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.
在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.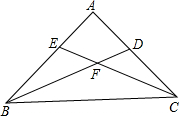 如图,在△ABC中,∠ABC、∠ACB的平分线相交于点F.
如图,在△ABC中,∠ABC、∠ACB的平分线相交于点F.