题目内容
10.已知在Rt△ABC中.(1)∠C=90°,tanA=$\frac{4}{3}$,BC=8,求AC;
(2)∠C=90°,若sinA+sinB=$\frac{7}{5}$,a+b=28,求c.
分析 (1)利用∠A的正切得到tanA=$\frac{BC}{AC}$=$\frac{4}{3}$,然后把BC=8代入可计算出AC的长;
(2)根据正弦的定义得到sinA=$\frac{a}{c}$,sinB=$\frac{b}{c}$,则sinA+sinB=$\frac{a+b}{c}$,所以$\frac{a+b}{c}$=$\frac{7}{5}$,然后把a+b=28代入计算即可得到c的值.
解答 解:(1)∵tanA=$\frac{BC}{AC}$=$\frac{4}{3}$,
∴AC=$\frac{3}{4}$BC=$\frac{3}{4}$×8=6;
(2)∵sinA=$\frac{a}{c}$,sinB=$\frac{b}{c}$,
∴sinA+sinB=$\frac{a+b}{c}$,
而sinA+sinB=$\frac{7}{5}$,
∴$\frac{a+b}{c}$=$\frac{7}{5}$,
∴c=$\frac{5}{7}$×28=20.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键的灵活运用勾股定理和锐角三角函数的定义.

练习册系列答案
相关题目
15.下列说法中,正确的是( )
| A. | 假命题的逆命题不一定是假命题 | |
| B. | 真命题的逆命题也是真命题 | |
| C. | 命题“若x>0,y<0,则xy<0”的逆命题是真命题 | |
| D. | 命题“对顶角相等”的逆命题是真命题 |
2.某单位假日组织员工到A地旅游,现雇一辆载19人(不能超载)的客车,而到A地旅游有甲、乙两条路可走.有关数据如下:
(1)设y1,y2(元)分别表示客车走甲、乙两条路线司机的收入,求y1,y2与乘客人数x(人)的关系式;
(2)通过以上情况分析,你若是司机,应该选择那一条路线?请作出函数图象加以说明.
| 路程/km | 每百千米耗油量/L | 油价 (元/L) | 过桥费/元 | 票价 元/人 | |
| 甲 | 60 | 14 | 3 | 20 | 16 |
| 乙 | 64 | 10 | 3 | 5 | 12 |
(2)通过以上情况分析,你若是司机,应该选择那一条路线?请作出函数图象加以说明.
20.将整式a3-16a分解因式,结果正确的是( )
| A. | a(a2-16) | B. | a(a+16)(a-1) | C. | a(a+16)(a-16) | D. | a(a+4)(a-4) |
 如图,在平行四边形ABCD中,AB=16,AD=10,BE=4,那么FC的长度是多少?
如图,在平行四边形ABCD中,AB=16,AD=10,BE=4,那么FC的长度是多少?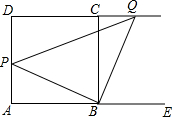 如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.
如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.