题目内容
13.今年上半年猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.(1)从今年2月起,猪肉价格不断走高,2月猪肉的平均价格为每千克25元,4月猪肉平均价格上涨到每千克36元,若3月、4月这两个月猪肉价格的增长率相同,求今年3月、4月猪肉价格的增长率;
(2)5月20日,猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的$\frac{3}{4}$,两种猪肉销售的总金额比5月20日提高了$\frac{1}{10}$a%,求a的值.
分析 (1)设今年3月、4月猪肉价格的增长率是x,则3月份的猪肉价格为:25(1+x);4月份的猪肉价格为:25(1+x)(1+x),又知4月份的猪肉价格36元,由此等量关系列出方程求出x的值,即求出了平均增长率;
(2)设5月20日两种猪肉总销量为1;根据题意列出方程,解方程即可.
解答 解:(1)设今年3月、4月猪肉价格的增长率是x,
依题意得:25(1+x)2=36,
解得x1=0.2=20%,x2=-2.2(舍去).
答:今年3月、4月猪肉价格的增长率是20%;
(2)设5月20日两种猪肉总销量为1;
根据题意得:40(1-a%)×$\frac{3}{4}$(1+a%)+40×$\frac{1}{4}$(1+a%)=40(1+$\frac{1}{10}$a%),
令a%=y,原方程化为:40(1-y)×$\frac{3}{4}$(1+y)+40×$\frac{1}{4}$(1+y)=40(1+$\frac{1}{10}$y),
整理得:5y2-y=0,
解得:y=0.2,或y=0(舍去),
则a%=0.2,
∴a=20;
答:a的值为20.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
8.下列方程的变形中,正确的是( )
| A. | 方程3x-2=2x+1,移项,得3x-2x=-1+2 | |
| B. | 方程3-x=2-5(x-1),去括号,得3-x=2-5x-1 | |
| C. | 方程$\frac{x-1}{0.2}$=$\frac{x}{0.5}$=1化成$\frac{x-1}{2}$=$\frac{x}{5}$=10 | |
| D. | 方程$\frac{2}{3}$x=$\frac{3}{2}$,未知数系数化为1,得x=$\frac{9}{4}$ |
3.下列计算正确的是( )
| A. | 2a2•a3=2a6 | B. | (3a2)3=9a6 | C. | a6÷a2=a3 | D. | (a2)3=a6 |
 如图△ABC中,AB=BC,∠B=36°,BC的垂直平分线DE交AB于D,垂足为E,试说明:BD=CD=AC.
如图△ABC中,AB=BC,∠B=36°,BC的垂直平分线DE交AB于D,垂足为E,试说明:BD=CD=AC.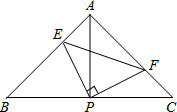 如图,在△ABC中,AB=AC,∠BAC=90°.直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( )
如图,在△ABC中,AB=AC,∠BAC=90°.直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( )