题目内容
17.利用勾股定理可以在数轴上画出表示$\sqrt{20}$的点,请依据以下思路完成画图,并保留画图痕迹:
第一步:(计算)尝试满足$\sqrt{20}$=$\sqrt{{a}^{2}+{b}^{2}}$,使其中a,b都为正整数,你取的正整数a=4,b=2;
第二步:(画长为$\sqrt{20}$的线段)以第一步中你所取的正整数a,b为两条直角边长画Rt△OEF,使O为原点,点E落在数轴的正半轴上,∠OEF=90°,则斜边OF的长即为$\sqrt{20}$,请在下面的数轴上画图;(第二步不要求尺规作图,不要求写画法)
第三步:(画表示$\sqrt{20}$的点)在下面的数轴上画出表示$\sqrt{20}$的点M,并描述第三步的画图步骤:以原点为圆心,OF为半径画弧交数轴的正半轴于点M,则点M为所作.
分析 第一步:利用实数的运算可确定a和b的值;
第二步:4对应的点为E点,过点E作数轴的垂线,再截取EF=2,然后连接OF,则OF=$\sqrt{20}$;
第三步:如图,在数轴的正半轴上截取OM=OF即可.
解答 解:第一步:a=4,b=2;
第二步:如图,OF为所作;
第三步:如图,以原点为圆心,OF为半径画弧交数轴的正半轴于点M,则点M为所作.
故答案为4,2;以原点为圆心,OF为半径画弧交数轴的正半轴于点M,则点M为所作.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.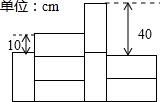 如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
 如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )| A. | 425cm2 | B. | 525cm2 | C. | 600cm2 | D. | 800cm2 |

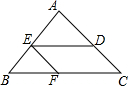 如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB,BC上,求△EBF的周长.
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB,BC上,求△EBF的周长. 宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫做黄金矩形.黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.请用尺规作图的方法在方格纸中作出一个黄金矩形(自己确定边的长度)
宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫做黄金矩形.黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.请用尺规作图的方法在方格纸中作出一个黄金矩形(自己确定边的长度)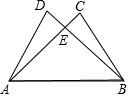 如图所示,AD=BC,AC=BD,试说明:DE=CE.
如图所示,AD=BC,AC=BD,试说明:DE=CE.