题目内容
6.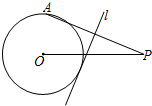 如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$.
如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$.
分析 连接OA、OC(C为切点),过点O作OB⊥AP.根据题意可知四边形BOCD为矩形,从而可知:BP=4+x,设AB的长为x,在Rt△AOB和Rt△OBP中,由勾股定理列出关于x的方程解得x的长,从而可计算出PA的长度.
解答 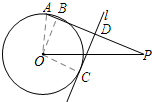 解:如图所示.连接OA、OC(C为切点),过点O作OB⊥AP.
解:如图所示.连接OA、OC(C为切点),过点O作OB⊥AP.
设AB的长为x,在Rt△AOB中,OB2=OA2-AB2=4-x2,
∵l与圆相切,
∴OC⊥l.
∵∠OBD=∠OCD=∠CDB=90°,
∴四边形BOCD为矩形.
∴BD=OC=2.
∵直线l垂直平分PA,
∴PD=BD+AB=2+x.
∴PB=4+x.
在Rt△OBP中,OP2=OB2+PB2,即4-x2+(4+x)2=52,解得x=$\frac{5}{8}$.
PA=2AD=2×($\frac{5}{8}$+2)=$\frac{21}{4}$.
故答案为$\frac{21}{4}$.
点评 本题主要考查的是勾股定理、切线的性质、矩形的性质和判定的综合应用,列出关于x的方程是解题的关键.

练习册系列答案
相关题目
1. 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( )
 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( )| A. | 100° | B. | 110° | C. | 120° | D. | 140° |
11. 在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
 在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )| A. | a | B. | 2b | C. | 2a-2b | D. | -2b |
18. 如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
 如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )| A. | 100° | B. | 130° | C. | 160° | D. | 150° |
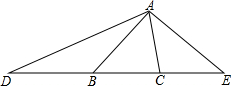 如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数. 如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?
如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?