题目内容
16.已知单项式-xy3,5x4y,-4y5,$\frac{2}{3}$x6y4,3x2y2,请你用这些单项式按下述要求解决问题:(1)写出一个五次三项式;
(2)这些单项式可以组成一个多项式,它是几次几项式,并把它按y的升幂重新排列.
分析 (1)直接利用多项式的次数与系数分析得出答案;
(2)根据多项式的项的概念和降幂排列的概念,可知多项式的项为:-xy3,5x4y,-4y5,$\frac{2}{3}$x6y4,3x2y2,将各项按y的指数由小到大排列可得.
解答 解:(1)可以为:-xy3+5x4y-4y5(答案不唯一);
(2)这些单项式可以组成一个多项式是十次五项式,
按y的升幂排列为:5x4y+3x2y2-xy3+$\frac{2}{3}$x6y4-4y5.
点评 本题考查了多项式的项的概念和降幂排列的概念.(1)多项式中的每个单项式叫做多项式的项;
(2)一个多项式的各项按照某个字母指数从大到小或者从小到大的顺序排列,叫做降幂或升幂排列.解题时要注意灵活运用.

练习册系列答案
相关题目
7.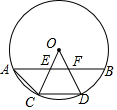 如图所示,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论:①OE=OF;②AC=CD=DB;③CD∥AB;④$\widehat{AC}$=$\widehat{BD}$,其中正确的有( )
如图所示,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论:①OE=OF;②AC=CD=DB;③CD∥AB;④$\widehat{AC}$=$\widehat{BD}$,其中正确的有( )
 如图所示,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论:①OE=OF;②AC=CD=DB;③CD∥AB;④$\widehat{AC}$=$\widehat{BD}$,其中正确的有( )
如图所示,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论:①OE=OF;②AC=CD=DB;③CD∥AB;④$\widehat{AC}$=$\widehat{BD}$,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.给定一列按规律排列的数;$\frac{1}{2}$,$\frac{2}{5}$,$\frac{3}{10}$,$\frac{4}{17}$,…,照此规律,则这列数的第6个数是( )
| A. | $\frac{5}{31}$ | B. | $\frac{6}{35}$ | C. | $\frac{6}{37}$ | D. | $\frac{7}{39}$ |
1.分式$\frac{x-2}{2x-6}$的值不存在,则x的取值是( )
| A. | x=-2 | B. | x=2 | C. | x=-3 | D. | x=3 |
8. 如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )
如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )
 如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )
如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )| A. | 75° | B. | 95° | C. | 105° | D. | 110° |
5.单项式-$\frac{2}{5}$ab3的系数和次数分别是( )
| A. | -$\frac{2}{5}$和3 | B. | $\frac{2}{5}$和3 | C. | -$\frac{2}{5}$和4 | D. | $\frac{2}{5}$和4 |
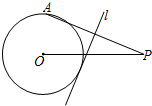 如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$.
如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$.