题目内容
15.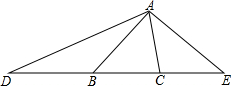 如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
分析 由题意知△ABD和△ACE均为等腰三角形,可由三角形内角和定理求得∠BAC的度数,用三角形的外角与内角的关系求得∠D与∠E的度数,即可求得∠DAE的度数.
解答 解:∵BD=BA,
∴∠D=∠DAB,
∵∠ABC=∠D+∠DAB,
∴∠D=∠DAB=$\frac{1}{2}$∠ABC=25°,
同理:∵AC=CE,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE,
∴∠E=∠CAE=$\frac{1}{2}$∠ACB=40°,
∴∠DAE=180°-40°-25°=115°.
点评 本题考查的是等腰三角形的性质,熟知等边对等角、三角形的外角与内角的关系、三角形的内角和定理是正确解答本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
5.单项式-$\frac{2}{5}$ab3的系数和次数分别是( )
| A. | -$\frac{2}{5}$和3 | B. | $\frac{2}{5}$和3 | C. | -$\frac{2}{5}$和4 | D. | $\frac{2}{5}$和4 |
7.若单项式-3a4m-nb2与$\frac{1}{3}$a3bm+n是同类项,则这两个单项式的积是( )
| A. | -a6b4 | B. | a6b4 | C. | -$\frac{8}{3}$a4b4 | D. | -a3b2 |
4.在数轴上与原点的距离等于5个单位的点表示的数是( )
| A. | 5 | B. | -5 | C. | 5和-5 | D. | 2和3 |
5.数据27.97米精确到0.1米得到的近似数为( )
| A. | 27.9米 | B. | 28米 | C. | 28.0米 | D. | 279.7米 |
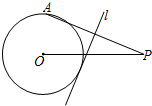 如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$.
如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$. 如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.
如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.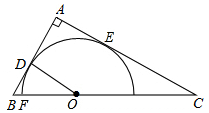 如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=4,AE=6,tan∠BOD=$\frac{2}{3}$.
如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=4,AE=6,tan∠BOD=$\frac{2}{3}$.