题目内容
18. 如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )| A. | 100° | B. | 130° | C. | 160° | D. | 150° |
分析 连接OA,根据三角形内角和定理求出∠ABC+∠ACB,根据线段垂直平分线的性质、等腰三角形的性质得到∠OAB=∠OBA,∠OAC=∠OCA,根据三角形内角和定理计算即可.
解答 解: 连接OA,
连接OA,
∵∠BAC=80°,
∴∠ABC+∠ACB=180°-80°=100°,
∵AB、AC的垂直平分线交于点O,
∴OB=OA,OC=OA,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠OBC+∠OCB=100°-(OBA+∠OCA)=20°,
∴∠BOC=180°-20°=160°,
故选:C.
点评 本题考查的是线段垂直平分线的性质、三角形内角和定理,掌握垂直平分线上任意一点,到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
8. 如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )
如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )
 如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )
如图,在△ABC中,∠A=60°,∠C=90°,CD是∠ACB的平分线,则∠BDC等于( )| A. | 75° | B. | 95° | C. | 105° | D. | 110° |
9.在为四川雅安地震的捐助活动中,某市共捐款3185800元,将3185800精确到十万位应表示为( )
| A. | 3.1×104 | B. | 3.1×105 | C. | 3.18×106 | D. | 3.2×106 |
7.若单项式-3a4m-nb2与$\frac{1}{3}$a3bm+n是同类项,则这两个单项式的积是( )
| A. | -a6b4 | B. | a6b4 | C. | -$\frac{8}{3}$a4b4 | D. | -a3b2 |
8.如果|a+2|+(b-1)2=0,那么(a+b)2013的值是( )
| A. | -2013 | B. | 2013 | C. | -1 | D. | 1 |
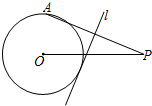 如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$.
如图,⊙O的半径为2,点P是⊙O外的一点,PO=5,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为$\frac{21}{4}$. 如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.
如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.