如图.一次函数与反比例函数的图象相交于A.B两点.则使得反比例函数值小于一次函数值的x的取值范围是( )A．x＜-1B．-1＜x＜0或x＞2C．x＜-1或0＜x＜2D．x＞2 题目和参考答案——青夏教育精英家教网—

题目内容

3．

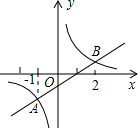如图，一次函数与反比例函数的图象相交于A、B两点，则使得反比例函数值小于一次函数值的x的取值范围是（　　）

A．

x＜-1

B．

-1＜x＜0或x＞2

C．

x＜-1或0＜x＜2

D．

x＞2

分析观察图形找出点A、B点的横坐标，结合两函数图象的上下位置关系以及点A、B的横坐标即可得出使得反比例函数值小于一次函数值的x的取值范围，此题得解．

解答解：观察函数图象发现：点A的横坐标为-1，点B的横坐标为2，
当-1＜x＜0或x＞2时，反比例函数图象在一次函数图象的下方，
∴使得反比例函数值小于一次函数值的x的取值范围是-1＜x＜0或x＞2．
故选B．

点评本题考查了反比例函数与一次函数的交点问题，根据两函数图象的上下位置关系找出反比例函数值小于一次函数值的x的取值范围是解题的关键．

练习册系列答案

14．已知实数a，b，c满足$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$=1，则$\frac{{a}^{2}}{b+c}$+$\frac{{b}^{2}}{c+a}$+$\frac{{c}^{2}}{a+b}$=0．

11．

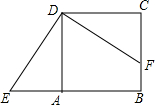如图，正方形ABCD中，点F在边BC上，E在边BA的延长线上．∠CDF=30°，若△DCF按顺时针方向旋转后恰好与△DAE重合．则最少旋转了（　　）度．

18．已知二次函数的图象与x轴的交点坐标是（-1，0），（5，0），且函数的最值是-3．则该抛物线开口向上，当x＞2时，y随的增大而增大．

8．下列计算正确的是（　　）

A．

$\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$

B．

（$\sqrt{5}$-$\sqrt{2}$）²=3

C．

（2-$\sqrt{5}$）（2+$\sqrt{5}$）=1

D．

$\frac{6-\sqrt{2}}{\sqrt{2}}$=3$\sqrt{2}$

15．计算：
（1）15+（-20）+6+（-8）；
（2）（-7）+8+3+（-6）+（-5）+9；
（3）3$\frac{3}{5}$+4$\frac{2}{5}$+（-5$\frac{2}{3}$）+（-$\frac{1}{3}$）；
（4）（-0.5）+2$\frac{1}{4}$+（-9$\frac{1}{2}$）+9.75．

12．用科学记数法表示下列各数
（1）900200
（2）300
（3）10000000
（4）-510000．

13．

已知二次函数y=ax²+bx+c的图象如图所示．
（1）这个二次函数的解析式为y=x²-2x；
（2）这个二次函数的对称轴是x=1；
（3）函数y有最小值，当x=1时，y的最值为-1；
（4）当x==-1或3时，y=3．

试题分类