题目内容
19.适合关于x的不等式组$\left\{\begin{array}{l}{2x+3<1}\\{x>\frac{1}{2}(x-3)}\end{array}\right.$的整数解是-2.分析 根据一元一次不等式组解出x的取值,根据x是整数解得出x的可能取值.
解答 解:$\left\{\begin{array}{l}2x+3<1①\\ x>\frac{1}{2}(x-3)②\end{array}\right.$
解①得2x<-2,即x<-1,
解②得2x>x-3,即x>-3,
综上可得-3<x<-1,
∵x为整数,故x=-2
故答案为:-2.
点评 本题考查了一元一次不等式组的整数解,解答本题的关键在于根据x的取值范围,得出x的整数解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.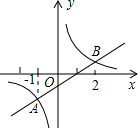 如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
 如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )| A. | x<-1 | B. | -1<x<0或x>2 | C. | x<-1或0<x<2 | D. | x>2 |
 如图所示,已知四边形ABCD和点O,画出四边形ABCD绕点O顺时针旋转90°后的图形.
如图所示,已知四边形ABCD和点O,画出四边形ABCD绕点O顺时针旋转90°后的图形. 一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.
一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.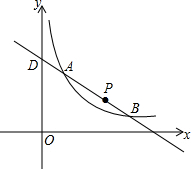 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,5)和点B(m,1).
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,5)和点B(m,1). 如图,∠1+∠2=180°,∠3=65°,求∠4的度数.
如图,∠1+∠2=180°,∠3=65°,求∠4的度数.