题目内容
13. 已知二次函数y=ax2+bx+c的图象如图所示.
已知二次函数y=ax2+bx+c的图象如图所示.(1)这个二次函数的解析式为y=x2-2x;
(2)这个二次函数的对称轴是x=1;
(3)函数y有最小值,当x=1时,y的最值为-1;
(4)当x==-1或3时,y=3.
分析 根据抛物线的对称轴性,抛物线的顶点坐标是(1,-1),利用待定系数法求抛物线的表达式则可.
解答 解:(1)根据题意,抛物线的顶点坐标是(1,-1),
设抛物线的表达式为y=a(x-1)2-1,
抛物线过(0,0),
所以a-1=0,a=1.
y=(x-1)2-1=x2-2x.
(2)∵y=(x-1)2-1,
∴对称轴是直线x=1;
(3)∵a=1,
∴数y有最小值,当x=1时,y的最值为-1;
(4)y=3时,x2-2x=3,
解得x=-1或3,
∴当x═-1或3时,y=3.
故答案为y=x2-2x;x=1;小,1,-1;-1或3.
点评 本题考查用待定系数法求二次函数解析式;会根据所给的函数值得到相应的自变量的值及取值.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
3.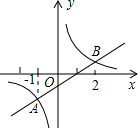 如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
 如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )| A. | x<-1 | B. | -1<x<0或x>2 | C. | x<-1或0<x<2 | D. | x>2 |
8.根据下列条件,能判定△ABC≌△A′B′C′的是( )
| A. | AB=A′B′,BC=B′C′,∠A=∠A′ | |
| B. | ∠A=∠A′,∠B=∠B′,AC=B′C′ | |
| C. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | |
| D. | AB=A′B′,BC=B′C′,△ABC的周长等于△A′B′C′的周长 |
5.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费=自来水销售费用+污水处理费用)
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a,b的值.
(2)小王家6月份交水费184元,则小王家6月份用水多少吨?
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
(1)求a,b的值.
(2)小王家6月份交水费184元,则小王家6月份用水多少吨?
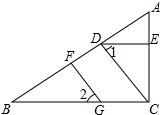 如图,若∠1=∠2,DE∥BC,则:①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )
如图,若∠1=∠2,DE∥BC,则:①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )