Question

1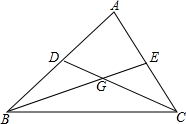．如图，△ABC中，∠A=60°，∠ACB的平分线CD和∠ABC的平分线BE交于点G，求证：BD+CE=BC．

Answer 1

分析 构造全等三角形，然后利用互补判断出∠CFG=∠CEG，得出△CFG≌△CEG即可．

解答 解：如图，
∵∠ACB的平分线CD和∠ABC的平分线BE交于点G，
∴∠ABC=2∠CBE，∠ACB=2∠BCD，
∵∠ABC+∠ACB+∠A=180°，
∴2∠CBE+2∠BCD+60°=180°，
∴∠CBE+∠BCD=60°，
∵∠CBE+∠BCD+∠BGC=180°，
∴∠BGC=180°-（∠CBE+∠BCD）=120°，
∴∠DBE=120°，
∵∠A=60°，
根据四边形的内角和是360°，得∠ADC+∠AEB=180°，
在BC上截取BF=BD，
在△BDG和△BFG中$\left\{\begin{array}{l}{BD=BF}\\{∠DBG=∠FBG}\\{BG=BG}\end{array}\right.$，
∴△BDG≌△BFG，
∴∠BDC=∠BFG，
∵∠BFG+∠CFG=180°，
∴∠BDC+∠CFG=180°
∵∠BDC+∠ADC=180°，
∴∠ADC=∠CFG，
∴∠CFG+∠AEB=180°，
∵∠AEB+∠CEG=180°，
∴∠CFG=∠CEG，
在△CFG和△CEG中$\left\{\begin{array}{l}{∠CFG=∠CEG}\\{∠FCG=∠ECG}\\{CG=CG}\end{array}\right.$，
∴△CFG≌△CEG，
∴CF=CE，
∴BC=BF+CF=BD+CE．

点评 此题是三角形全等的判定和性质，主要考查了同角或等角的补角相等，邻补角，三角形和四边形的内角和，角平分线的定义，解本题的关键是∠CFG=∠CEG，难点是构造全等三角形．