题目内容
13.关于x的分式方程$\frac{2x+m}{x-3}$=-2解为正数,则m的取值范围是m<6且m≠-6.分析 先去分母,用m表示x,求出m的范围
解答 解:去分母得,2x+m=-2x+6,
∴x=$\frac{6-m}{4}$,
∵分式方程的解为正数,
∴$\frac{6-m}{4}$>0且$\frac{6-m}{4}$≠3
∴m<6且m≠-6,
故答案为:m<6且m≠-6.
点评 此题是分式方程的解,考查了分式方程的解法,及正数的意义,解本题的关键是解分式方程.

练习册系列答案
相关题目
16.将代数式x2-6x+2化为(x+p)2+q的形式为( )
| A. | (x-3)2+11 | B. | (x+3)2-7 | C. | (x-3)2-7 | D. | (x+3)2+11 |
3. 甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为S甲2、S乙2,下列关系正确的是( )
甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为S甲2、S乙2,下列关系正确的是( )
 甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为S甲2、S乙2,下列关系正确的是( )
甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.设他们这10次射击成绩的方差为S甲2、S乙2,下列关系正确的是( )| A. | S甲2<S乙2 | B. | S甲2>S乙2 | C. | S甲2=S乙2 | D. | 无法确定 |
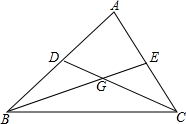 如图,△ABC中,∠A=60°,∠ACB的平分线CD和∠ABC的平分线BE交于点G,求证:BD+CE=BC.
如图,△ABC中,∠A=60°,∠ACB的平分线CD和∠ABC的平分线BE交于点G,求证:BD+CE=BC.

