题目内容
已知二次函数y=ax2+bx+c,且不等式ax2+bx+c>-2x的解为1<x<3
(1)若方程ax2+bx+c+6a=0有两个相等的根,求二次函数的表达式;
(2)若y=ax2+bx+c的最大值为正数,求a的取值范围.
(1)若方程ax2+bx+c+6a=0有两个相等的根,求二次函数的表达式;
(2)若y=ax2+bx+c的最大值为正数,求a的取值范围.
考点:抛物线与x轴的交点,二次函数的最值
专题:
分析:(1)根据题意得出二次函数y=ax2+bx+c的图象和直线y=-2x的交点为(1,-2),(3,-6),再根据方程ax2+bx+c+6a=0有两个相等的根得出关于a、b、c的方程组,解方程组即可求得a、b、c的值,进而求得解析式.
(2)先求得b=-2-4a,c=3a,根据题意b2-4ac>0,把b=-2-4a,c=3a代入即可求得a的取值.
(2)先求得b=-2-4a,c=3a,根据题意b2-4ac>0,把b=-2-4a,c=3a代入即可求得a的取值.
解答:解:(1)∵不等式ax2+bx+c>-2x的解为1<x<3,
∴二次函数y=ax2+bx+c的图象和直线y=-2x的交点为(1,-2),(3,-6),
根据题意得
,
解得
或
(不合题意,舍去),
∴二次函数的表达式为y=-
x2-
x-
.
(2))∵不等式ax2+bx+c>-2x的解为1<x<3,
∴二次函数y=ax2+bx+c的图象和直线y=-2x的交点为(1,-2),(3,-6),a<0,
∴
∴b=-2-4a,c=3a,
∵y=ax2+bx+c的最大值为正数,
∴b2-4ac>0,
即(-2-4a)2-4a•3a>0,解得a>-2+
或a<-2-
.
所以a的取值为a>-2+
或a<-2-
.
∴二次函数y=ax2+bx+c的图象和直线y=-2x的交点为(1,-2),(3,-6),
根据题意得
|
解得
|
|
∴二次函数的表达式为y=-
| 1 |
| 5 |
| 6 |
| 5 |
| 3 |
| 5 |
(2))∵不等式ax2+bx+c>-2x的解为1<x<3,
∴二次函数y=ax2+bx+c的图象和直线y=-2x的交点为(1,-2),(3,-6),a<0,
∴
|
∴b=-2-4a,c=3a,
∵y=ax2+bx+c的最大值为正数,
∴b2-4ac>0,
即(-2-4a)2-4a•3a>0,解得a>-2+
| 3 |
| 3 |
所以a的取值为a>-2+
| 3 |
| 3 |
点评:本题考查了二次函数与x轴的交点,待定系数法求解析式,主要运用的是方程的根与系数的关系.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
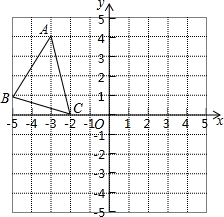 已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2.
已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2.