题目内容
5.正方形的边长为a,当边长增加1时,其面积增加了2a+1.分析 根据正方形的面积公式进行解答即可.
解答 解:∵正方形的边长为a,
∴其面积=a2.
∵正方形的边长为a,当边长增加1时其边长为a+1,
∴其面积=(a+1)2,
∴(a+1)2-a2=a2+2a+1-a2=2a+1.
故答案为:2a+1.
点评 本题考查的是完全平方公式,熟知(a±b)2=a2±2ab+b2是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.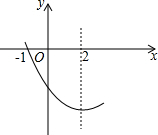 如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
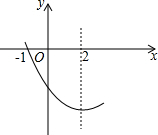 如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )| A. | ①②③ | B. | ③④⑤ | C. | ②④⑤ | D. | ①③④⑤ |
14.一元一次不等式-3x<12的解集是( )
| A. | x<4 | B. | x>4 | C. | x<-4 | D. | x>-4 |
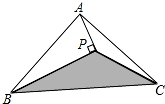 如图,△ABC的面积为1cm2,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为0.5cm2.
如图,△ABC的面积为1cm2,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为0.5cm2. 某矿泉水厂生产一种矿泉水,经侧算,用一吨水生产的矿泉水所获利润y(元)与1吨水的价格x(元)的关系如图所示.
某矿泉水厂生产一种矿泉水,经侧算,用一吨水生产的矿泉水所获利润y(元)与1吨水的价格x(元)的关系如图所示.