题目内容
17.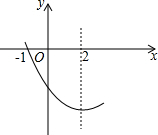 如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤若点(-3,y1),(-6,y2)都在抛物线上,则y1<y2.其中正确的是( )| A. | ①②③ | B. | ③④⑤ | C. | ②④⑤ | D. | ①③④⑤ |
分析 根据抛物线的图象,数形结合,逐一解析判断,即可解决问题.
解答 解:∵抛物线的对称轴为x=2,
∴-$\frac{b}{2a}$=2,b=-4a,4a+b=0,故③正确;
∵抛物线开口向上,
∴a>0,b<0;由图象知c<0,
∴abc>0,故①正确;
由抛物线的单调性知:当x=-2时,y>0,
即4a-2b+c>0,故②错误;
∵$\frac{-1+5}{2}$=2,而对称轴方程为 x=2,
∴抛物线与x轴的另一个交点是(5,0),故④正确.
∵-6<-2<2,
∴由抛物线的单调性知:y1<y2,故⑤正确;
故正确结论为:①③④⑤.
故选D.
点评 该题主要考查了二次函数的图象与系数的关系、抛物线的单调性、对称性及其应用问题;灵活运用有关知识来分析、解答是关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
12.下列一组数:-108,6.6,-|-3|,-π,-$\frac{22}{7}$,0.1010010001中,无理数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.下列命题中,真命题的个数有( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等.
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,已知点A(4,0)、B(0,2),∠AOB的平分线交AB于C.动点M从O点出发,以每秒2个单位长度的速度沿x轴向点A作匀速运动,同时动点N从O点出发,以每秒1个单位长度的速度沿y轴向点B作匀速运动,点P、Q为点M、N关于直线OC的对称点,设M运动的时间为t(0<t<2)秒.
如图,已知点A(4,0)、B(0,2),∠AOB的平分线交AB于C.动点M从O点出发,以每秒2个单位长度的速度沿x轴向点A作匀速运动,同时动点N从O点出发,以每秒1个单位长度的速度沿y轴向点B作匀速运动,点P、Q为点M、N关于直线OC的对称点,设M运动的时间为t(0<t<2)秒.