题目内容
14.已知正三角形的面积是$\frac{3}{4}\sqrt{3}$cm,则正三角形外接圆的半径是1cm.分析 如图,⊙O为等边△ABC的外接圆,设⊙O的半径为r,作AH⊥BC于H,根据等边三角形的性质得BH=CH,∠BAH=30°,利用垂径定理的推理可判断点O在AH上,连结OB,则∠BOH=2∠BAO=60°,利用含30度的直角三角形三边的关系可得OH=$\frac{1}{2}$OB=$\frac{1}{2}$r,BH=$\sqrt{3}$OH=$\frac{\sqrt{3}}{2}$r,则BC=2BH=$\sqrt{3}$r,然后根据三角形面积公式得到$\frac{1}{2}$•(r+$\frac{1}{2}$r)•$\sqrt{3}$r=$\frac{3\sqrt{3}}{4}$,再解方程即可.
解答 解:如图,⊙O为等边△ABC的外接圆,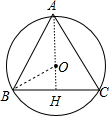 设⊙O的半径为r,
设⊙O的半径为r,
作AH⊥BC于H,
∵△ABC为等边三角形,AH⊥BC,
∴BH=CH,∠BAH=30°,
∴点O在AH上,
连结OB,则∠BOH=2∠BAO=60°,
∴OH=$\frac{1}{2}$OB=$\frac{1}{2}$r,BH=$\sqrt{3}$OH=$\frac{\sqrt{3}}{2}$r,
∴BC=2BH=$\sqrt{3}$r,
∵正三角形的面积是$\frac{3}{4}\sqrt{3}$cm,
∴$\frac{1}{2}$AH•BC=$\frac{3\sqrt{3}}{4}$,即$\frac{1}{2}$•(r+$\frac{1}{2}$r)•$\sqrt{3}$r=$\frac{3\sqrt{3}}{4}$,
∴r=1,
即正三角形外接圆的半径是1cm.
故答案为1.
点评 本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.解决本题的关键是灵活应用等边三角形的性质.

 阅读快车系列答案
阅读快车系列答案 如图,正六边形ABCDEF内接于圆O,圆O的半径为6,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于圆O,圆O的半径为6,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )| A. | 3、$\frac{π}{3}$ | B. | $\frac{3}{2}$$\sqrt{3}$、π | C. | 3$\sqrt{3}$、$\frac{2π}{3}$ | D. | 3$\sqrt{3}$、2π |
| A. |  | B. |  | C. |  | D. |  |
| A. | a+1 | B. | $\frac{1}{a+1}$ | C. | a-1 | D. | $\frac{a}{a-1}$ |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
| A. | -30 | B. | -20 | C. | -5 | D. | 0 |
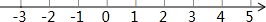 解不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}+1≥2}\\{3x-1≤2(x+1)}\end{array}\right.$,请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}+1≥2}\\{3x-1≤2(x+1)}\end{array}\right.$,请结合题意填空,完成本题的解答.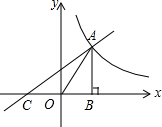 如图,已知一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为4,则AC的长为4$\sqrt{2}$(保留根号).
如图,已知一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为4,则AC的长为4$\sqrt{2}$(保留根号).