题目内容
19.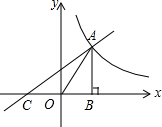 如图,已知一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为4,则AC的长为4$\sqrt{2}$(保留根号).
如图,已知一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为4,则AC的长为4$\sqrt{2}$(保留根号).
分析 由于△AOB的面积为4,根据反比例函数的比例系数k的几何意义可知k=8,解由y=x+2与y=$\frac{8}{x}$联立起来的方程组,得出A点坐标,又易求点C的坐标,从而利用勾股定理求出AC的长.
解答 解:∵点A在反比例函数y=$\frac{k}{x}$的图象上,AB⊥x轴于点B,△AOB的面积为4,
∴k=8.
解方程组$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{8}{x}}\end{array}\right.$,
得$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
∴A(2,4);
在y=x+2中,令y=0,得x=-2.
∴C(-2,0).
∴AB=4,BC=4,
∴AC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
故答案为4$\sqrt{2}$.
点评 本题考查函数图象交点坐标的求法及反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=$\frac{1}{2}$|k|.

练习册系列答案
相关题目
10.一个角的余角是30°,则这个角的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
7. 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
4. 如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
 如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )
如图,矩形ABCD和矩形CEFG中,AD=2,AB=1,CE=3,EF=6,连接AF,H是AF的中点,那么CH的长是( )| A. | $\frac{5}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{2}$$\sqrt{2}$ | D. | 2 |
9.实数4的算术平方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 4 |
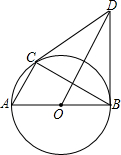 如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.
如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.
 如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.
如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.