题目内容
4. 如图,正六边形ABCDEF内接于圆O,圆O的半径为6,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于圆O,圆O的半径为6,则这个正六边形的边心距OM和$\widehat{BC}$的长分别为( )| A. | 3、$\frac{π}{3}$ | B. | $\frac{3}{2}$$\sqrt{3}$、π | C. | 3$\sqrt{3}$、$\frac{2π}{3}$ | D. | 3$\sqrt{3}$、2π |
分析 连接OC,OD,由正六边形ABCDEF可求出∠COD=60°,进而可求出∠COM=30°,根据30°角的锐角三角函数值即可求出边心距OM的长,再由弧长公式即可求出弧BC的长.
解答 解: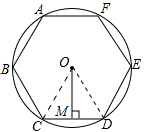 连接OC,OD,
连接OC,OD,
∵正六边形ABCDEF是圆的内接多边形,
∴∠COD=60°,
∵OC=OD,OM⊥CD,
∴∠COM=30°,
∵OC=6,
∴OM=6cos30°=3$\sqrt{3}$,
∴$\widehat{BC}$=$\frac{60×π×6}{180}$=2π
故选D.
点评 本题考查了正多边形和圆、正六边形的性质、等腰三角形的判定与性质以及弧长公式的运用,熟练掌握正六边形的性质是解决问题的关键.

练习册系列答案
相关题目
14.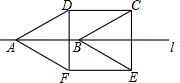 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
12.下列四个数中,相反数是-$\frac{1}{5}$的数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | -$\frac{1}{5}$ |
19.据大连市公安局统计,2016年全市约有410000人换二代居民身份证,将410000用科学记数法表示应为( )
| A. | 0.41×104 | B. | 41×104 | C. | 4.1×106 | D. | 4.1×105 |
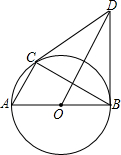 如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.
如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.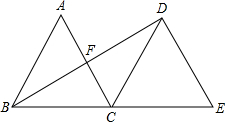 如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长是2$\sqrt{3}$.
如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长是2$\sqrt{3}$.