Question

2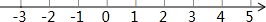．解不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}+1≥2}\\{3x-1≤2（x+1）}\end{array}\right.$，请结合题意填空，完成本题的解答．
（1）解不等式①，得x≥-1；
（2）解不等式②，得x≤3；
（3）把不等式①和②的解集在数轴上表示出来；
（4）原不等式组的解集为-1≤x≤3．

Answer 1

分析 （1）首先去分母、然后移项、合并同类项即可求解；
（2）去括号、移项、合并同类项即可求解；
（3）不等式的解集表示在数轴上即可；
（4）根据（3）即可直接写出不等式组的解集．

解答 解：（1）去分母，得x+3+2≥4，
移项，得x≥4-2-3，
合并同类项，得x≥-1，
故答案是：x≥-1；
（2）去括号，得3x-1≤2x+2，
移项，得3x-2x≤2+1，
合并同类项，得x≤3，
故答案是：x≤3；
（3）
；
（4）不等式组的解集是：-1≤x≤3．
故答案是：-1≤x≤3．

点评 本题考查了不等式组的解法，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．