题目内容
9. 如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上两点,连接AE、CF、DF,满足EA=CA.
如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上两点,连接AE、CF、DF,满足EA=CA.(1)求证:AE是⊙O的切线;
(2)若⊙O的半径为3,tan∠CFD=$\frac{4}{3}$,求AD的长.
分析 (1)连接OA,OE,易证△AOC≌△AOE(SSS),从而可知∠OEA=∠ACB=90°,所以AE是⊙O的切线.
(2)连接CD,因为∠CBA=∠CFD,所以tan∠CBA=tan∠CFD=$\frac{4}{3}$,从而可求出AC=8,利用勾股定理即可求出AB=10,再证明△ADC∽△ACB,从而可求出AD的长度.
解答 解:(1)连接OA,OE,
在△AOC与△AOE中,
$\left\{\begin{array}{l}{AC=AE}\\{OC=OE}\\{OA=OA}\end{array}\right.$
∴△AOC≌△AOE(SSS)
∴∠OEA=∠ACB=90°,
∴OE⊥AE,
∴AE是⊙O的切线
(2)连接CD
∵∠CBA=∠CFD
∴tan∠CBA=tan∠CFD=$\frac{4}{3}$,
∵在Rt△ACB中,
tan∠CBA=$\frac{CA}{CB}$=$\frac{CA}{6}$=$\frac{4}{3}$
∴AC=8
∴由勾股定理可知:AB=10,
∵BC为⊙O的直径,
∴∠CDB=∠ADC=90°,
∵∠ADC=∠ACB,∠DAC=∠CAB,
∴△ADC∽△ACB
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,
∴AD=6.4
点评 本题考查圆的综合问题,涉及全等三角形的性质与判定,相似三角形的性质与判定,勾股定理,圆周角定理等知识,综合程度较高,属于中等题型.

练习册系列答案
相关题目
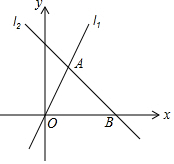 如图,在平面直角坐标系xOy中,直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(2,4),直线l2与x轴交于点B(6,0).
如图,在平面直角坐标系xOy中,直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(2,4),直线l2与x轴交于点B(6,0).
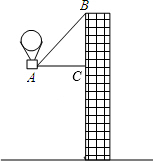 如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)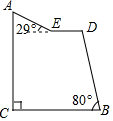 “蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)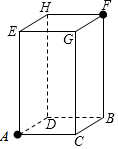 一只蚂蚁如果沿长方体的表面从A点爬到F点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
一只蚂蚁如果沿长方体的表面从A点爬到F点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.