题目内容
4.先化简,再选一个你喜欢的a的值代入求值:$\frac{2}{a-1}$+$\frac{{a}^{2}-4a+4}{{a}^{2}-1}$÷$\frac{a-2}{a+1}$.分析 根据分式的除法和加法可以化简题目中的式子,然后选取一个使得原分式有意义的x的值代入即可解答本题.
解答 解:$\frac{2}{a-1}$+$\frac{{a}^{2}-4a+4}{{a}^{2}-1}$÷$\frac{a-2}{a+1}$
=$\frac{2}{a-1}+\frac{(a-2)^{2}}{(a+1)(a-1)}•\frac{a+1}{a-2}$
=$\frac{2}{a-1}+\frac{a-2}{a-1}$
=$\frac{a}{a-1}$,
当a=0时,原式=$\frac{0}{0-1}=0$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
| 日期x | 1 | 2 | 3 | 4 |
| 水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
13.某登山队从大本营出发,在向上攀登的过程中,测得所在位置的气温y℃与向上攀登的高度x km的几组对应值如表:
若每向上攀登1km,所在位置的气温下降幅度基本一致,则向上攀登的海拔高度为2.5km时,登山队所在位置的气温约为-10℃.
| 向上攀登的高度x/km | 0.5 | 1.0 | 1.5 | 2.0 |
| 气温y/℃ | 2.0 | -0.9 | -4.1 | -7.0 |
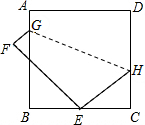 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,求线段EC,CH的长.
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,求线段EC,CH的长. 如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上两点,连接AE、CF、DF,满足EA=CA.
如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上两点,连接AE、CF、DF,满足EA=CA.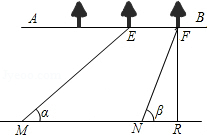 综合实践课,小明所在小组要测量护城河的宽度,如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°.请你根据这些数据帮小明他们算出河宽FR(结果保留整数).
综合实践课,小明所在小组要测量护城河的宽度,如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°.请你根据这些数据帮小明他们算出河宽FR(结果保留整数).