题目内容

20．将图1中五边形纸片ABCDE的A点以BE为折线往下折，A点恰好落在CD上，如图2所示，再分别以图2的AB，AE为折线，将C，D两点往上折，使得A、B、C、D、E五点均在同一平面上，如图3所示，若图1中∠A=124°，则图3中∠CAD的度数为何（　　）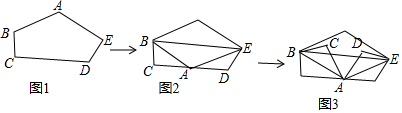
A．56B．60C．62D．68

分析 根据三角形内角和定理和折叠的性质来解答即可．

解答 解：由图（2）知，∠BAC+∠EAD=180°-124°=56°，
所以图（3）中∠CAD=180°-56°×2=68°．
故选：D．

点评 本题考查了多边形内角与外角，结合图形解答，需要学生具备一定的读图能力和空间想象能力．

练习册系列答案
相关题目
10．（1）计算：$\sqrt{\frac{4}{9}}$-$\sqrt{（-2）^{4}}$+$\root{3}{\frac{8}{27}}$-（-1）2017；
（2）求满足条件（x-2）2=9的x值．
11．如果|x-3|+（y+1）2=0，则x-y=4．
8．符合数轴所表示的解集的不等式组是（　　）
A．$\left\{\begin{array}{l}{x+1＞0}\\{4-x＞0}\end{array}\right.$B．$\left\{\begin{array}{l}{x+1＞0}\\{x-4＞0}\end{array}\right.$C．$\left\{\begin{array}{l}{x+1＜0}\\{x-4＞0}\end{array}\right.$D．$\left\{\begin{array}{l}{x+1＜0}\\{4-x＞0}\end{array}\right.$
15．计算：
（1）（-48a6b5c）÷（24ab4）•（-$\frac{5}{6}$a5b2）；
（2）已知xm=3，xn=2，求x2m-3n的值；
（3）已知6x=5y，求代数式（x-3y）2-（x-y）（x+y）-5y2的值．
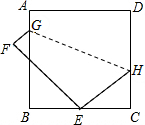5．如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，求线段EC，CH的长．
12．$\frac{x}{x-1}$=$\frac{2}{{{x^2}-1}}$+1．
9．如图，Rt△ABC中，∠ACB=90°，以BC为直径的⊙O交AB于点D，E、F是⊙O上两点，连接AE、CF、DF，满足EA=CA．
（1）求证：AE是⊙O的切线；
（2）若⊙O的半径为3，tan∠CFD=$\frac{4}{3}$，求AD的长．
20．对于任意整数n，多项式（4n+5）2-9都能（　　）
A．被6整除B．被7整除C．被8整除D．被6或8整除

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网