题目内容
如图,在平面直角坐标系中,将抛物线y=
x2先向右平移1个单位,再向下平移
个单位,得到新的抛物线y=ax2+bx+c,该抛物线与y轴交于点B,与x轴正半轴交于点C.
(1)求点B和点C的坐标;
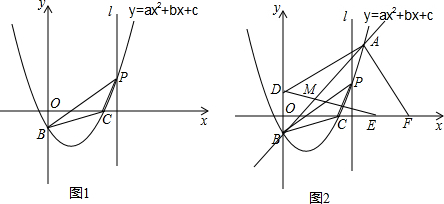
(2)如图1,有一条与y轴重合的直线l向右匀速平移,移动的速度为每秒1个单位,移动的时间为t秒,直线l与抛物线y=ax2+bx+c交于点P,当点P在x轴上方时,求出使△PBC的面积为2
的t值;
(3)如图2,将直线BC绕点B逆时针旋转,与x轴交于点M(1,0),与抛物线y=ax2+bx+c交于点A,在y轴上有一点D(0,
),在x轴上另取两点E,F(点E在点F的左侧),EF=2,线段EF在x轴上平移,当四边形ADEF的周长最小时,先简单描述如何确定此时点E的位置?再直接写出点E的坐标.
| ||
| 3 |
4
| ||
| 3 |
(1)求点B和点C的坐标;
(2)如图1,有一条与y轴重合的直线l向右匀速平移,移动的速度为每秒1个单位,移动的时间为t秒,直线l与抛物线y=ax2+bx+c交于点P,当点P在x轴上方时,求出使△PBC的面积为2
| 3 |
(3)如图2,将直线BC绕点B逆时针旋转,与x轴交于点M(1,0),与抛物线y=ax2+bx+c交于点A,在y轴上有一点D(0,
2
| ||
| 3 |

考点:二次函数综合题
专题:压轴题
分析:(1)根据条件即可写出新抛物线的解析式,然后只需令x=0就可得到点B的坐标,令y=0就可得到点C的坐标;
(2)过点P作PH⊥y轴于点H,如图1,则有PH=t,然后运用割补法表示出△BCP的面积,根据条件“△PBC的面积为2
”可用t的代数式表示出OH,从而得到点P的坐标(用t的代数式表示),然后将点P的坐标代入新抛物线的解析式就可解决问题;
(3)由于AD、EF是定值,要使四边形ADEF的周长最小,只需DE+AF最小,由于DE与AF不相连,可将AF向左平移2个单位到A′E,从而将问题转化为DE+EA′最小,可作点D关于x轴的对称点D′,则有D′E=DE,从而将问题转化为D′E+EA′最小,根据两点之间线段最短可知当D′、E、A′三点共线时,D′E+EA′最小;要求四边形ADEF的周长最小时对应的点E的坐标,只需依次求出直线BM的解析式、点A的坐标,点A′的坐标,点D关于x轴的对称点D′的坐标,直线A′D′的解析式,直线A′D′与x轴的交点E′的坐标,就可解决问题.
(2)过点P作PH⊥y轴于点H,如图1,则有PH=t,然后运用割补法表示出△BCP的面积,根据条件“△PBC的面积为2
| 3 |
(3)由于AD、EF是定值,要使四边形ADEF的周长最小,只需DE+AF最小,由于DE与AF不相连,可将AF向左平移2个单位到A′E,从而将问题转化为DE+EA′最小,可作点D关于x轴的对称点D′,则有D′E=DE,从而将问题转化为D′E+EA′最小,根据两点之间线段最短可知当D′、E、A′三点共线时,D′E+EA′最小;要求四边形ADEF的周长最小时对应的点E的坐标,只需依次求出直线BM的解析式、点A的坐标,点A′的坐标,点D关于x轴的对称点D′的坐标,直线A′D′的解析式,直线A′D′与x轴的交点E′的坐标,就可解决问题.
解答:解:(1)将抛物线y=
x2先向右平移1个单位,再向下平移
个单位,
得到新的抛物线的解析式为y=
(x-1)2-
.
当x=0时,y=
-
=-
,则点B的坐标为(0,-
);
令y=0,得
(x-1)2-
=0,
解得:x1=3,x2=-1,
∵点C在x轴正半轴上,
∴点C的坐标为(3,0);
(2)过点P作PH⊥y轴于点H,如图1,
由题可得PH=1×t=t.
∵点B(0,-
),点C(3,0),
∴OB=
,OC=3,
∴S△BCP=S梯形PHOC+S△BOC-S△PHB
=
(PH+OC)•OH+
OB•OC-
BH•PH
=
(t+3)•OH+
×
×3-
(OH+
)•t
=
OH+
-
t=2
,
解得:OH=
t+
,
∴点P的坐标为(t,
t+
).
∵点P在抛物线y=
(x-1)2-
上,
∴
(t-1)2-
=
t+
,
解得:t1=4,t2=-1
∵点P在第一象限,
∴t=4;

(3)将点A向左平移2个单位到点A′,作点D关于x轴的对称点D′,连接A′D′,交x轴于点E′,
当点E运动到点E′时,四边形ADEF的周长最小,此时点E的坐标为(
,0).
解题思路如下:
先用待定系数法求出BM的解析式,为y=
x-
,
然后将直线BM与抛物线的解析式组成方程组,求出它们的一个交点A的坐标,为(5,4
),
从而可得点A向左平移2个单位所对应的点A′的坐标,为(3,4
),
由点D(0,
)可得到该点关于x轴的对称点D′的坐标,为(0,-
),
然后运用待定系数法求出直线A′D′的解析式,为y=
x-
,
然后令y=0,就可得到直线A′D′与x轴的交点E′的坐标,为(
,0).
| ||
| 3 |
4
| ||
| 3 |
得到新的抛物线的解析式为y=
| ||
| 3 |
4
| ||
| 3 |
当x=0时,y=
| ||
| 3 |
4
| ||
| 3 |
| 3 |
| 3 |
令y=0,得
| ||
| 3 |
4
| ||
| 3 |
解得:x1=3,x2=-1,
∵点C在x轴正半轴上,
∴点C的坐标为(3,0);
(2)过点P作PH⊥y轴于点H,如图1,
由题可得PH=1×t=t.
∵点B(0,-
| 3 |
∴OB=
| 3 |

∴S△BCP=S梯形PHOC+S△BOC-S△PHB
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
=
| 3 |
| 2 |
3
| ||
| 2 |
| ||
| 2 |
| 3 |
解得:OH=
| ||
| 3 |
| ||
| 3 |
∴点P的坐标为(t,
| ||
| 3 |
| ||
| 3 |
∵点P在抛物线y=
| ||
| 3 |
4
| ||
| 3 |
∴
| ||
| 3 |
4
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
解得:t1=4,t2=-1
∵点P在第一象限,
∴t=4;

(3)将点A向左平移2个单位到点A′,作点D关于x轴的对称点D′,连接A′D′,交x轴于点E′,
当点E运动到点E′时,四边形ADEF的周长最小,此时点E的坐标为(
| 3 |
| 7 |
解题思路如下:
先用待定系数法求出BM的解析式,为y=
| 3 |
| 3 |
然后将直线BM与抛物线的解析式组成方程组,求出它们的一个交点A的坐标,为(5,4
| 3 |
从而可得点A向左平移2个单位所对应的点A′的坐标,为(3,4
| 3 |
由点D(0,
2
| ||
| 3 |
2
| ||
| 3 |
然后运用待定系数法求出直线A′D′的解析式,为y=
14
| ||
| 9 |
2
| ||
| 3 |
然后令y=0,就可得到直线A′D′与x轴的交点E′的坐标,为(
| 3 |
| 7 |
点评:本题主要考查了抛物线上点的坐标特征、用待定系数法求直线的解析式、平移的性质、两点之间线段最短等知识,运用割补法是解决第(2)小题的关键,通过平移变换将不相连的两条线段之和转化为相连的两条线段之和是解决第(3)小题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥DE,∠A=120°,C=80°,则∠D的度数为( )
如图,AB∥DE,∠A=120°,C=80°,则∠D的度数为( )| A、130° | B、120° |
| C、160° | D、145° |
在不透明的布袋中,装有大小、形状完全相同的3个黑球、1个红球,从中摸一个球,摸出1个黑球这一事件是( )
| A、必然事件 | B、随机事件 |
| C、确定事件 | D、不可能事件 |
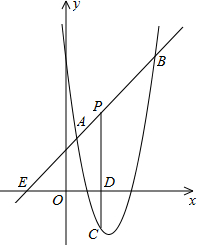 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(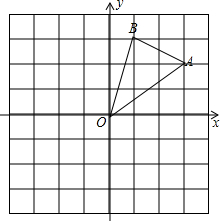 如图,在边长为1的正方形组成的网格中,△AOB的顶点圴在格点上,其中A(3,2)、B(1,3)
如图,在边长为1的正方形组成的网格中,△AOB的顶点圴在格点上,其中A(3,2)、B(1,3) 如图,一次函数y=(m-1)x+3的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为
如图,一次函数y=(m-1)x+3的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为