题目内容
2. 如图,P为半径R的⊙O直径AB上的任意一点,弦CD经过点P,且∠APD=45°,已知PC2+PD2的值是一个定值,那么这个定值是2R2.
如图,P为半径R的⊙O直径AB上的任意一点,弦CD经过点P,且∠APD=45°,已知PC2+PD2的值是一个定值,那么这个定值是2R2.
分析 连接OD,作OE⊥CD于E,根据垂径定理得到DE=$\frac{1}{2}$CD,根据勾股定理得到CD2=4R2-2OP2,根据相交弦定理得到PC•PD=R2-OP2,运用完全平方公式计算得到答案.
解答 解: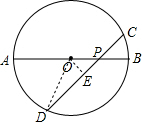 连接OD,作OE⊥CD于E,
连接OD,作OE⊥CD于E,
则DE=$\frac{1}{2}$CD,
∴CD2=4DE2=4(R2-OE2),
∵∠APD=45°,
∴OE=$\frac{\sqrt{2}}{2}$OP,
∴CD2=4DE2=4(R2-$\frac{1}{2}$OP2)=4R2-2OP2,
∵PC•PD=PB•PA=(R-OP)(R+OP)=R2-OP2,
PC2+PD2=(PC+PD)2-2PC•PD
=4R2-2OP2-2(R2-OP2)
=2R2.
故答案为:2R2.
点评 本题考查的是垂径定理、相交弦定理和勾股定理,正确作出辅助线、构造直角三角形、灵活运用定理是解题的关键.

练习册系列答案
相关题目
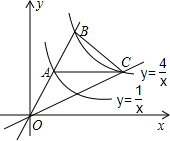 如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3.
如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3. 已知:反比例函数y=$\frac{2}{x}$与一次函数交于点A,D,一次函数与x轴、y轴分别交于点C,B,求证:AB=CD.
已知:反比例函数y=$\frac{2}{x}$与一次函数交于点A,D,一次函数与x轴、y轴分别交于点C,B,求证:AB=CD.