题目内容
17.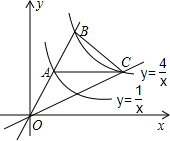 如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3.
如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3.
分析 过B作BD⊥x轴于D,C作CE⊥x轴于E,则BD∥CE,设B(m,$\frac{4}{m}$),C(n,$\frac{4}{n}$),于是得到A($\frac{n}{4}$,$\frac{4}{n}$),求得BD=$\frac{4}{m}$,CE=$\frac{4}{n}$,DE=n-m,AC=n-$\frac{n}{4}$=$\frac{3n}{4}$,由于S△OBC=S△ACO+S△ABC=S梯形BDEC,得到方程$\frac{1}{2}$×$\frac{3n}{4}$×$\frac{4}{n}$+$\frac{1}{2}×$$\frac{3n}{4}$×($\frac{4}{m}$-$\frac{4}{n}$)=$\frac{1}{2}×$($\frac{4}{n}+\frac{4}{m}$)(n-m),解得n=2m,于是得到结论.
解答 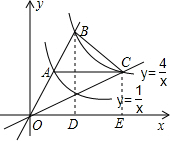 解:过B作BD⊥x轴于D,C作CE⊥x轴于E,
解:过B作BD⊥x轴于D,C作CE⊥x轴于E,
则BD∥CE,
设B(m,$\frac{4}{m}$),C(n,$\frac{4}{n}$),
∵AC∥x轴,
∴A($\frac{n}{4}$,$\frac{4}{n}$),
∴BD=$\frac{4}{m}$,CE=$\frac{4}{n}$,DE=n-m,AC=n-$\frac{n}{4}$=$\frac{3n}{4}$,
∵S△OBC=S△ACO+S△ABC=S梯形BDEC,
∴$\frac{1}{2}$×$\frac{3n}{4}$×$\frac{4}{n}$+$\frac{1}{2}×$$\frac{3n}{4}$×($\frac{4}{m}$-$\frac{4}{n}$)=$\frac{1}{2}×$($\frac{4}{n}+\frac{4}{m}$)(n-m),
解得:n=2m,
∴S△OBC=S梯形BDEC=$\frac{1}{2}$×$\frac{6}{m}$×m=3,
故答案为:3,
点评 本题考查了反比例函数系数k的几何意义,三角形的面积,梯形的面积,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案
 如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分.
如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分. 如图,P为半径R的⊙O直径AB上的任意一点,弦CD经过点P,且∠APD=45°,已知PC2+PD2的值是一个定值,那么这个定值是2R2.
如图,P为半径R的⊙O直径AB上的任意一点,弦CD经过点P,且∠APD=45°,已知PC2+PD2的值是一个定值,那么这个定值是2R2. 如图,四边形AOBC是平行四边形,A(-2,0),B(4,2$\sqrt{3}$),反比例函数y=$\frac{n}{x}$的图象经过点C.
如图,四边形AOBC是平行四边形,A(-2,0),B(4,2$\sqrt{3}$),反比例函数y=$\frac{n}{x}$的图象经过点C. 如图所示,在四边形ABCD中,DC∥AB,DN=CN,AM=BM,DC=5,AB=11,∠A+∠B=90°,则MN=3.
如图所示,在四边形ABCD中,DC∥AB,DN=CN,AM=BM,DC=5,AB=11,∠A+∠B=90°,则MN=3.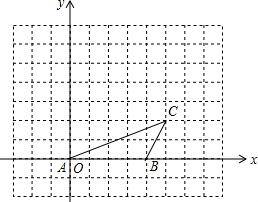 如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.