在数学中.为了简便.记$\sum {k=1}^{n}$k=1+2+3+-+(n-1)+n.又记1!=1.2!=2×1.3!=3×2×1.-.n!=n××-×3×2×1．则$\sum {k=1}^{2014}$k-$\sum {k=1}^{2015}$+$\frac{2015!}{2014!}$=0．题目和参考答案——青夏教育精英家教网—

题目内容

16．在数学中，为了简便，记$\sum_{k=1}^{n}$k=1+2+3+…+（n-1）+n，又记1!=1，2!=2×1，3!=3×2×1，…，n!=n×（n-1）×（n-2）×…×3×2×1．则$\sum_{k=1}^{2014}$k-$\sum_{k=1}^{2015}$+$\frac{2015!}{2014!}$=0．

分析原式利用题中的新定义化简，计算即可得到结果．

解答解：根据题中的新定义得：原式=1+2+…+2014-（1+2+…+2015）+$\frac{2015×2014×2013×…×1}{2014×2013×…×1}$=-2015+2015=0，
故答案为：0

点评此题考查了有理数的混合运算，弄清题中的新定义是解本题的关键．

练习册系列答案

相关题目

6．

已知二次函数y=ax²+bx+c的图象如图所示，则a的取值范围为（　　）

$\frac{1}{2}$＜a＜$\frac{5}{8}$

7．如图，某包装厂用一种矩形纸饭制作无盖长方体纸盒，已知将一张此种矩形纸板的四个角各剪去边长为10cm的正方形后，剩下部分刚好能围成一个容积为8000cm³的无盖长方体纸盒，且此长方纸盒的底面长比宽多20cm．求这种纸板的长和宽．

4．

如图，⊙O中，半径OA⊥半径OB，C是$\widehat{AB}$上任一点，则∠A+∠B=135°．

11．计算：（8x⁵y²-4x³y+3x²y²）÷（-$\frac{3}{2}$xy）

1．用配方法求下列抛物线的顶点坐标：
（1）y=x²+4x+7．
（2）y=-2x²-4x+1．

8．已知a、b、c是△ABC的三边长．求证：关于x的方程b²x²+（b²+c²-a²）x+c²=0没有实数根．

5．

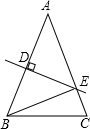如图，在△ABC中，AC=8cm，AB的垂直平分线交AB于点D，交边AC于点E，EC=2cm，则BE的长为（　　）

2．

如图，P为半径R的⊙O直径AB上的任意一点，弦CD经过点P，且∠APD=45°，已知PC²+PD²的值是一个定值，那么这个定值是2R²．

试题分类