题目内容
1. 如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
分析 连接CD,构建全等三角形,证明△ECD≌△FBD即可.
解答  解:连接CD,
解:连接CD,
∵∠C=90°,D是AB的中点,
∴CD=$\frac{1}{2}$AB=BD,
∵AC=BC,
∴CD⊥AB,∠ACD=∠B=45°,
∴∠CDF+∠BDF=90°,
∵ED⊥DF,
∴∠EDF=90°,
∴∠EDC+∠CDF=90°,
∴∠EDC=∠BDF,
∴△ECD≌△FBD,
∴DE=DF.
点评 本题考查了等腰直角三角形和全等三角形的性质和判定,运用了直角三角形斜边上的中线等于斜边的一半,以及等腰三角形三线合一的性质,同时要熟知等腰直角三角形的特殊性:如两个锐角都是45°;在全等三角形的证明中,常运用同角的余角相等来证明角相等.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
19.在等式y=kx+b中,当x=-1时,y=0;当x=0时,y=-1,则这个等式是( )
| A. | y=x-1 | B. | y=x+1 | C. | y=-x-1 | D. | y=-x+1 |
 已知直线y1=2x+2及直线y2=-x+5,.
已知直线y1=2x+2及直线y2=-x+5,. 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且(a-3)2+$\sqrt{{b}^{2}-10b+25}$=0.
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且(a-3)2+$\sqrt{{b}^{2}-10b+25}$=0.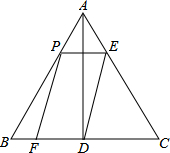 如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6).
如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6).
 已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.