题目内容
11. 已知直线y1=2x+2及直线y2=-x+5,.
已知直线y1=2x+2及直线y2=-x+5,.(1)直线y2=-x+5与y轴的交点坐标为(0,5).
(2)在所给的平面直角坐标系(如图)中画出这两条直线的图象;
(3)求这两条直线以及x轴所围成的三角形面积.
分析 (1)令x=0求得y值后即可确定交点坐标;
(2)利用描点法作出函数的图象即可;
(3)首先求得两直线的交点坐标,然后求得与两坐标轴的交点坐标,利用三角形的面积计算公式进行计算即可.
解答 解:(1)在y2=-x+5中,令x=0,可得y2=5,
∴直线y2=-x+5与y轴的交点坐标为(0,5),
故答案为:(0,5);
(2)在y1=2x+2中,令x=0,可得y1=2,令y1=0,可得x=-1,
∴直线y1与y轴交于点A(0,2),与x轴交于点B(-1,0);
在y2=-x+5中,令y2=0,可求得x=5,
∴直线y2与x轴交于点C(5,0),且由(1)可知与y轴交于点D(0,5),
联立两直线解析式可得$\left\{\begin{array}{l}{y=2x+2}\\{y=-x+5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,
∴两直线的交点E(1,4),
∴两直线的图象如图所示;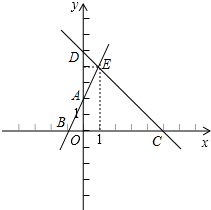
(3)由(2)可知BC=5-(-1)=6,…(7分)
且E到BC的距离为4,
∴S△BCE=$\frac{1}{2}$×6×4=12;
点评 考查了两条直线平行或相交的问题,解题的关键是了解如何求得两个直线的交点坐标,难度不大.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
6.某商家计划从厂家采购空调和冰箱两种产品共20台,空调和冰箱的采购单价与销售单价如表所示:
(1)若采购空调12台,且所采购的空调和冰箱全部售完,求商家的利润;
(2)厂家有规定,采购空调的数量不少于10台,且空调采购单价不低于1200元,问商家采购空调多少台时总利润最大?并求最大利润.
| 采购单价 | 销售单价 | |
| 空调 | -20x+1500 | 1760 |
| 冰箱 | -10x+1300 | 1700 |
(2)厂家有规定,采购空调的数量不少于10台,且空调采购单价不低于1200元,问商家采购空调多少台时总利润最大?并求最大利润.
3.面积为4cm2的正方形,对角线的长为( )cm.
| A. | 4 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 6 |
 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG. 如图,在?ABCD中,E为AD中点,CE交BA延长线于F,
如图,在?ABCD中,E为AD中点,CE交BA延长线于F, 如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.