题目内容
7.已知,把Rt△ABC和Rt△DEF按图1摆放,(点C与E点重合),点B、C、E、F始终在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8,BC=6,EF=10,如图2,△DEF从图1的位置出发,以每秒1个单位的速度沿CB向△ABC匀速移动,同时,点P从A出发,沿AB以每秒1个单位向点B匀速移动,AC与△DEF的直角边相交于Q,当P到达终点B时,△DEF同时停止运动.连接PQ,设移动的时间为t(s).解答下列问题:(1)△DEF在平移的过程中,当点D在Rt△ABC的AC边上时,求t的值;
(2)在移动的过程中,是否存在△APQ为等腰三角形?若存在,求出t的值;若不存在,说明理由.
(3)在移动的过程中,当0<t≤5时,连接PE,是否存在△PQE为直角三角形?若存在,求出t的值;若不存在,说明理由.

分析 (1)作出辅助线,计算出HC=5,即可;
(2)分情况讨论.先分成0≤t≤5和5<t≤10两种,每一种又要按边分情况讨论分AP=AQ,AP=PQ,AQ=PQ.即可;
(3)由△PQE为直角三角形,所以按直角顶点分三种情况,再利用相似,找出相等关系,求解即可.
解答 解:(1)作DH⊥EF于H.如图1,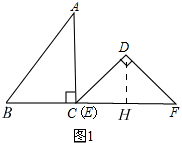
在Rt△ABC中,
∵∠ACB=90°,AC=8,BC=6
∴AB=$\sqrt{{8}^{2}{+6}^{2}}$=10
∵∠EDF=90°,∠DEF=45°
∴∠F=45°
∴HE=HF=$\frac{1}{2}$EF=5
∴t=5 即t=5s时,点D在AC边上.
(2)①当0≤t≤5,即直角边DE与AC相交于Q点时,
由题意知:AP=CE=CQ=t
∴AQ=8-t
(ⅰ)当AP=AQ时,t=8-t
解得t=4
(ⅱ)当PA=PQ时,作PM⊥AQ于M,
则AM=QM=$\frac{1}{2}$AQ=$\frac{1}{2}$(8-t)
经探索:△APM∽△ABC
∴$\frac{AP}{AB}=\frac{AM}{AC}$
即 $\frac{t}{10}=\frac{AM}{8}$
∴AM=$\frac{4}{5}$t,
∴$\frac{4}{5}$t=$\frac{1}{2}$(8-t)
解得t=$\frac{40}{13}$,
(ⅲ)当QP=QA时,作QN⊥AP于N,
则AN=PN=$\frac{1}{2}$AP=$\frac{1}{2}$t,
经探索:△AQN∽△ABC
∴$\frac{AN}{AC}=\frac{AQ}{AB}$ 即 $\frac{\frac{1}{2}t}{8}=\frac{8-t}{10}$∴t=$\frac{64}{13}$
②当5<t≤10时,即直角边DF与AC相交于Q点时,
由题意知:AP=CE=t,CQ=CF=10-t,PB=10-t,AQ=t-2
(ⅰ) 当AP=AQ时,
∵t≠t-2
∴不存在
(ⅱ)当QA=QP时,作QG⊥AP于G,
则PG=AG=$\frac{1}{2}$AP=$\frac{1}{2}$t
经探索:△AQG∽△ABC
∴$\frac{AQ}{AB}=\frac{AG}{AC}$
即$\frac{t-2}{10}=\frac{\frac{1}{2}t}{8}$
∴t=$\frac{16}{3}$
(ⅲ)当PA=PQ时,作PI⊥AQ于I,
则AI=QI=$\frac{1}{2}$AQ=$\frac{1}{2}$(t-2)
经探索:△API∽△ABC
∴$\frac{AP}{AB}=\frac{AI}{AC}$
即$\frac{t}{10}\frac{\frac{1}{2}(t-2)}{8}$
∴t=-$\frac{10}{3}$(舍去)
综上所述:当t=4,$\frac{40}{13}$,$\frac{64}{13}$,$\frac{16}{3}$时,△APQ是等腰三角形.
(3)①当∠PQE=90°时,作PH⊥AQ于H
∵∠ACB=90°,∠DEF=45°
∴∠CQE=45°
∴∠PQH=45°
∴PH=QH
∵AP=t
∴PH=$\frac{3}{5}$t,AH=$\frac{4}{5}$t,
又∵CQ=CE=t
∴$\frac{3}{5}$t=8-t-$\frac{4}{5}$t
解得t=$\frac{10}{3}$
②当∠PEQ=90°时,作PG⊥BC于G,
∵∠QEC=45°
∴∠PEG=45°
∴PG=GE
∵AP=t
∴PB=10-t
∴BG=$\frac{3}{5}$(10-t),PG=$\frac{4}{5}$(10-t)
∴$\frac{4}{5}$(10-t)=6-$\frac{3}{5}$(10-t)-t
解得t=20(不合题意,舍去)
③当∠QPE=90°时,作QM⊥AB于M,EN⊥AB于N,
∵AP=CE=CQ=t
∴PB=10-t,AQ=8-t,BE=6-t
∵△BNE∽△BCA
∴BN=$\frac{3}{5}$(6-t),NE=$\frac{4}{5}$(6-t),PN=10-t-$\frac{3}{5}$(6-t)
∵△AMQ∽△ACB
∴AM=$\frac{4}{5}$(8-t),QM=$\frac{3}{5}$(8-t),PM=t-$\frac{4}{5}$(8-t)
经探索:△PNE∽△QMP
∴$\frac{PN}{QM}=\frac{NE}{MP}$即$\frac{10-t-\frac{3}{5}(6-t)}{\frac{3}{5}(8-t)}=\frac{\frac{4}{5}(6-t)}{t-\frac{4}{5}(8-t)}$
t1=4 t2=$\frac{40}{3}$(舍去)
综上所述,存在$\frac{10}{3}$或4时,△PQE为直角三角形.
点评 此题是几何变换综合题,主要考查等腰三角形和直角三角形的性质,分情况是解本题的关键.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | 1.74×106 | B. | 1.73×106 | C. | 17.4×105 | D. | 17.3×105 |
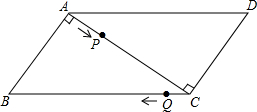 已知,如图,用两块一样大的直角三角板拼成一个平行四边形,∠BAC=∠ACD=90°.在?ABCD中,AB=3cm,BC=5cm,点P自A向C、沿AC的方向匀速运动,速度为1cm/s;同时,点Q从点C出发,自C向B、沿CB方向匀速运动,速度为1cm/s;过点P作PM⊥AD,并与AD相交于点M,当P、Q中有一个点到达终点时,另一个点也停止运动.设运动时间为t(s).解答下列问题:
已知,如图,用两块一样大的直角三角板拼成一个平行四边形,∠BAC=∠ACD=90°.在?ABCD中,AB=3cm,BC=5cm,点P自A向C、沿AC的方向匀速运动,速度为1cm/s;同时,点Q从点C出发,自C向B、沿CB方向匀速运动,速度为1cm/s;过点P作PM⊥AD,并与AD相交于点M,当P、Q中有一个点到达终点时,另一个点也停止运动.设运动时间为t(s).解答下列问题: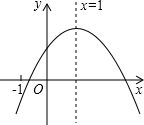 二次函数图象如图所示,对称轴为x=1,给出下列结论:
二次函数图象如图所示,对称轴为x=1,给出下列结论: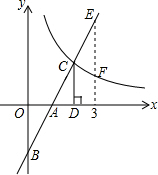 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论: