题目内容
17.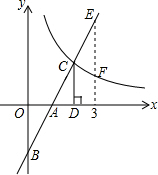 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①S△ADB=S△ADC;②当0<x<3时,y1<y2;③如图,当x=3时,EF=$\frac{8}{3}$;④方程2x2-2x-k=0有解.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据题意可以求得AD、OA的长,点C和点B的坐标,从而可以求出△ADB和△ADC的面积,从而可以判断该结论是否正确;
②根据函数图象可以判断该结论是否正确;
③根据函数图象可以得到0<x<3时,两个函数的大小情况,从而可以判断该结论是否成立;
④根据两个函数图象有交点,然后联立方程组可知有解,通过变形可以得到方程2x2-2x-k=0,从而可以判断该结论是否正确.
解答 解:将x=0代入y1=2x-2得,y=-2;将y=0代入y1=2x-2得x=1,
即点A的坐标为(1,0),点B的坐标为(0,-2),
∵OA=AD,
∴点D的坐标是(2,0),
将x=2代入y1=2x-2得,y=2,
∴点C的坐标是(2,2),
∴${S}_{△ADB}=\frac{AD×OB}{2}=\frac{1×2}{2}=1$,${S}_{△ADC}=\frac{AD•CD}{2}=\frac{1×2}{2}=1$,故①正确;
由图象可知,当0<x<2时,y1<y2,当x>2时,y1>y2;故②错误;
∵点C(2,2)在双曲线y2=$\frac{k}{x}$上,
∴$2=\frac{k}{2}$,得k=4,
∴双曲线y2=$\frac{4}{x}$,
将x=3代入双曲线y2=$\frac{4}{x}$,得y=$\frac{4}{3}$;将x=3代入y1=2x-2得y=4,
∴EF=$4-\frac{4}{3}=\frac{8}{3}$,故③正确;
由图象可知,y1=2x-2与y2=$\frac{k}{x}$在第一象限有解,
∴2x-2=$\frac{k}{x}$有解,
即2x2-2x-k=0有解,故④正确;
由上可得,①③④正确.
故选C.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案| A. | k<0 | B. | k<-1 | C. | k<-2 | D. | k<-3 |
| A. | 675×102 | B. | 67.5×102 | C. | 6.75×104 | D. | 6.75×105 |
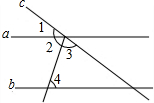 如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )| A. | 54° | B. | 58° | C. | 63° | D. | 68° |

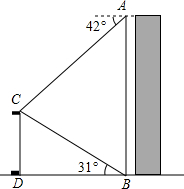 如图,某校数学兴趣小组在楼AB的顶部A处测得该楼正前方旗杆CD的顶端C的俯角为42°,在楼AB的底部B处测得旗杆CD的顶端C的仰角为31°,已知旗杆CD的高度为12m,根据测得的数据,计算楼AB的高度(结果保留整数).
如图,某校数学兴趣小组在楼AB的顶部A处测得该楼正前方旗杆CD的顶端C的俯角为42°,在楼AB的底部B处测得旗杆CD的顶端C的仰角为31°,已知旗杆CD的高度为12m,根据测得的数据,计算楼AB的高度(结果保留整数).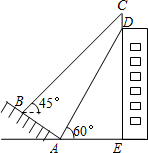 如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)