题目内容
9.先化简,再求值:$\frac{{x}^{2}-9}{{x}^{2}-3x}$÷(6+$\frac{{x}^{2}+9}{x}$),其中x=$\sqrt{3}$-1.分析 先把括号内通分,再把除法运算化为乘法运算,约后后得到$\frac{1}{x+3}$,然后把x的值代入计算即可.
解答 解:$\frac{{x}^{2}-9}{{x}^{2}-3x}$÷(6+$\frac{{x}^{2}+9}{x}$),
=$\frac{{x}^{2}-9}{{x}^{2}-3x}$÷$\frac{6x+{x}^{2}+9}{x}$,
=$\frac{(x+3)(x-3)}{x(x-3)}$•$\frac{x}{(x+3)^{2}}$,
=$\frac{1}{x+3}$;
当x=$\sqrt{3}$-1时,原式=$\frac{1}{\sqrt{3}-1+3}$=$\frac{1}{\sqrt{3}+2}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$.
点评 本题考查了分式的化简求值:先把分式的分子或分母因式分解,再进行通分或约分,得到最简分式或整式,然后把满足条件的字母的值代入计算得到对应的分式的值.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
19.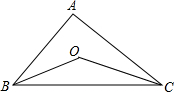 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )| A. | 140° | B. | 120° | C. | 90° | D. | 80° |
14.为了了解某班学生每天使用零花钱的情况,随机调查了15名同学,结果如下,下列说法正确的是( )
| 每天零花钱(元) | 0 | 5 | 10 | 15 | 20 |
| 人数 | 2 | 3 | 2 | 6 | 2 |
| A. | 众数是20元 | B. | 平均数是11元 | C. | 极差是15元 | D. | 中位数是10元 |
1.在-2,-5,5,0这四个数中,最小的数是( )
| A. | -2 | B. | -5 | C. | 5 | D. | 0 |
18.计算(-a2)3+(-a3)2的结果是( )
| A. | -2a5 | B. | 0 | C. | 2a5 | D. | -2a6 |

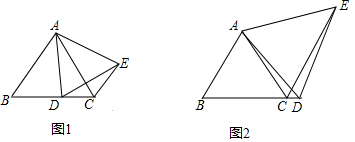
 如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )