题目内容
19.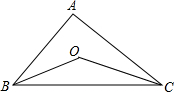 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )| A. | 140° | B. | 120° | C. | 90° | D. | 80° |
分析 先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠OBC+∠OCB的度数,由三角形内角和定理即可得出结论.
解答 解:∵在△ABC中,∠A=100°,
∴∠ABC+∠ACB=180°-100°=80°,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×80°=40°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-40°=140°.
故选A.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
7.设a、b互为相反数,c、d互为倒数,则2016(a+b)-cd的值是( )
| A. | 2016 | B. | 0 | C. | 1 | D. | -1 |
14.在Rt△ABC中,∠C=90°,∠A=30°,AB=8cm,则BC=( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
4.若a+b+c=0,且abc≠0,则a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{a}$+$\frac{1}{c}$)+c($\frac{1}{a}$+$\frac{1}{b}$)的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | -3 |
11.下列事件中,属于必然事件的是( )
| A. | 打开电视机正在播放广告 | |
| B. | 投掷一枚质地均匀的硬币100次,正面向上的次数为50次 | |
| C. | 任意一个二次函数图象与x轴必有交点 | |
| D. | 任意画一个三角形,其内角和为180° |
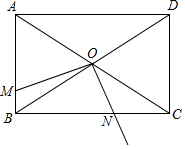 如图,O为矩形ABCD对角线的交点,M为AB边上任一点,射线ON⊥OM于点O,且与BC边交于点N,若AB=4,AD=6,则四边形OMBN面积的最大值为$\frac{23}{3}$.
如图,O为矩形ABCD对角线的交点,M为AB边上任一点,射线ON⊥OM于点O,且与BC边交于点N,若AB=4,AD=6,则四边形OMBN面积的最大值为$\frac{23}{3}$.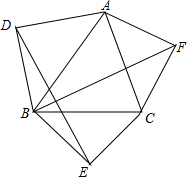 如图,以△ABC三边为底向外作等腰直角三角形,连接DE、BF.
如图,以△ABC三边为底向外作等腰直角三角形,连接DE、BF.