如图.∠1.∠2.∠3.∠4满足的关系是( )A．∠1+∠2=∠3+∠4B．∠1+∠2=∠4-∠3C．∠1+∠4=∠2+∠3D．∠1+∠4=∠2-∠3 题目和参考答案——青夏教育精英家教网——

题目内容

15．

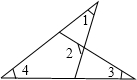如图，∠1、∠2、∠3、∠4满足的关系是（　　）

A．

∠1+∠2=∠3+∠4

B．

∠1+∠2=∠4-∠3

C．

∠1+∠4=∠2+∠3

D．

∠1+∠4=∠2-∠3

分析如图，由三角形外角的性质可得∠1+∠4=∠5，∠2=∠5+∠3，整理可求得∠1、∠2、∠3、∠4满足的关系．

解答解：
如图，由三角形外角的性质可得∠1+∠4=∠5，∠2=∠5+∠3，
∴∠1+∠4=∠2-∠3，
故选D．

点评本题主要考查三角形外角性质，掌握三角形一个外角等于不相邻两个内角的和是解题的关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

2．已知：y=y₁+y₂，y₁与x成正比例，y₂与x成反比例，且x=1时，y=3，x=-2时，y=-$\frac{9}{2}$，求x=-$\frac{1}{2}$时，y的值．

6．在直线AB上任取一点O，过点O作射线OC、OD，使∠COD=90°，当∠AOC=40°时，∠BOD的度数是（　　）

3．a=5¹⁴⁰，b=3²¹⁰，c=2²⁸⁰，则a、b、c的大小关系是（　　）

10．船在静水中的速度为10km/h，水流速度为2km/h，顺流航行s km所需时间为（　　）

（$\frac{s}{10}$+2）h

（$\frac{s}{10+2}$）h

（$\frac{s}{10}$-2）h

（$\frac{s}{10-2}$）h

20．为了估计池塘两岸A、B间的距离，杨阳在池塘的一侧选取了一点P，测得PA=14m，PB=11m，那么AB间的距离不可能是（　　）

为了加强视力保护意识，小明要在书房里挂一张视力表．由于书房空间狭小，他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表．如图，如果大视力表中“E”的高度是3.5cm，那么小视力表中相应“E”的高度是（　　）

如图，△ABC中，∠C=90°，CD⊥AB于D，图中线段中可以作为△ACD的高的有（　　）

5．已知，在△ABC中，AD为BC边上的中线，AC=5，AD=4，则AB的取值范围是（　　）