题目内容
2.已知:y=y1+y2,y1与x成正比例,y2与x成反比例,且x=1时,y=3,x=-2时,y=-$\frac{9}{2}$,求x=-$\frac{1}{2}$时,y的值.分析 首先假设y1=ax,y2=$\frac{b}{x}$,进而把x=1时,y=3,x=-2时,y=-$\frac{9}{2}$,求出a,b的值,进而得出答案.
解答 解:∵y=y1+y2,y1与x成正比例,y2与x成反比例,
∴设y1=ax,y2=$\frac{b}{x}$,
则y=ax+$\frac{b}{x}$,把x=1时,y=3,x=-2时,y=-$\frac{9}{2}$代入得:
$\left\{\begin{array}{l}{a+b=3}\\{-2a-\frac{b}{2}=-\frac{9}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
则y=2x+$\frac{1}{x}$,
当x=-$\frac{1}{2}$时,y=2×(-$\frac{1}{2}$)+$\frac{1}{-\frac{1}{2}}$=-3.
点评 此题主要考查了待定系数法求反比例函数以及正比例函数解析式,正确假设出解析式是解题关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12.等式(1-x)( )=1-x2中,括号内应填入( )
| A. | x-1 | B. | 1-x | C. | 1+x | D. | -1-x |
13.下列说法中,正确的是( )
| A. | 两条射线组成的图形叫做角 | |
| B. | 直线l经过点A,那么点A在直线l上 | |
| C. | 把一个角分成两个角的射线叫角的平分线 | |
| D. | 若AB=BC,则点B是线段AC的中点 |
10.若点D,E分别为△ABC中AB,AC的中点,且AB=6,AC=8,BC=10,则DE的长为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 12 |
14.某市为提倡节约用水,采取分段收费,若用户每月用水不超过20立方米,每立方米收费2元;若用水超过20立方米,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水量为( )
| A. | 34立方米 | B. | 32立方米 | C. | 30立方米 | D. | 28立方米 |
15.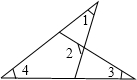 如图,∠1、∠2、∠3、∠4满足的关系是( )
如图,∠1、∠2、∠3、∠4满足的关系是( )
 如图,∠1、∠2、∠3、∠4满足的关系是( )
如图,∠1、∠2、∠3、∠4满足的关系是( )| A. | ∠1+∠2=∠3+∠4 | B. | ∠1+∠2=∠4-∠3 | C. | ∠1+∠4=∠2+∠3 | D. | ∠1+∠4=∠2-∠3 |

 如图,直线y=-$\frac{3}{4}$x-6分别与y轴、x轴交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在y轴上的点B处,则直线AM的解析式为y=-2x-6.
如图,直线y=-$\frac{3}{4}$x-6分别与y轴、x轴交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在y轴上的点B处,则直线AM的解析式为y=-2x-6.