题目内容
9. 如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则sin∠EDB的值是( )
如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则sin∠EDB的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{5}$ | D. | $\frac{1}{5}$ |
分析 由于所求的∠EDB是圆周角,因此可将其转化到另外一个圆周角来求解,设圆O与小正方形网格的另外一个切点为F,连接EF、BF、BE,因此∠EDB=∠EFB=45°,所以sin∠EDB=$\frac{\sqrt{2}}{2}$.
解答 解: 设圆O与小正方形网格的另一个切点为F,连接BF、BE,
设圆O与小正方形网格的另一个切点为F,连接BF、BE,
∵$\widehat{EB}=\widehat{EB}$,
∴∠EDB=∠EFB,
由题意知:EB=BF,
∴∠EFB=45°,
∴sin∠EDB=sin∠EFB=$\frac{\sqrt{2}}{2}$,
故答案选(B)
点评 本题考查圆周角定理的应用,如若条件出现的角是圆周角,可考虑圆周角定理将其转移到适合的位置进行求解.

练习册系列答案
相关题目
20.若-$\frac{a}{2}$<-$\frac{a}{3}$,则a一定满足是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
17.方程4x2+4x+1=0的解是( )
| A. | x1=x2=2 | B. | x1=x2=$\frac{1}{2}$ | C. | x1=x2=-2 | D. | x1=x2=-$\frac{1}{2}$ |
4.爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下
9:00时看到的两位数是( )
| 时刻 | 9:00 | 9:45 | 12:00 |
| 碑上的数 | 是一个两位数,数字之和是9 | 十位与个位数字与9:00时所看到的正好相反 | 比9:00时看到的两位数中间多了个0 |
| A. | 54 | B. | 45 | C. | 36 | D. | 27 |
1.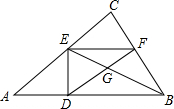 如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
 如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )| A. | t=$\frac{14}{17}$ | B. | t=$\frac{12}{10}$ | C. | t=$\frac{10}{17}$ | D. | t=$\frac{8}{17}$ |
 如图,在平面直角坐标系xOy中,直线l:y=kx-3k(k<0)与x、y轴的正半轴分别交于点A、B,动点D(异于点A、B)在线段AB上,DC⊥x轴于C.
如图,在平面直角坐标系xOy中,直线l:y=kx-3k(k<0)与x、y轴的正半轴分别交于点A、B,动点D(异于点A、B)在线段AB上,DC⊥x轴于C. 已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S.
已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S. 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论: