题目内容
19. 阅读下面材料:
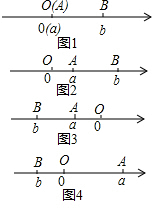
阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,AB=OB=|b|=|a-b|
当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=a-b=|a-b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|;
综上,数轴上A、B两点之间的距离|AB|=|a-b|.
回答下列问题:
①数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4;
②数轴上表示x和-1的两点A和B之间的距离是|x+1|,如果|AB|=2,那么x为1或-3;
③当代数式|x+4|+|y-7|取最小值时,则x-y=-11.
分析 ①根据数轴上A、B两点之间的距离|AB|=|a-b|,分别求出数轴上表示2和5的两点之间的距离、数轴上表示-2和-5的两点之间的距离、数轴上表示1和-3的两点之间的距离各是多少即可.
②根据数轴上A、B两点之间的距离|AB|=|a-b|,求出数轴上表示x和-1的两点A和B之间的距离是|x+1|,然后根据|AB|=2,可得|x+1|=2,据此求出x的值是多少即可.
③当代数式|x+4|+|y-7|取最小值时,|x+4|=0,|y-7|=0,据此求出x、y的值各是多少,然后把求出的x、y的值代入,求出算式x-y的值是多少即可.
解答 解:①数轴上表示2和5的两点之间的距离是:|2-5|=3,
数轴上表示-2和-5的两点之间的距离是:|-2-(-5)|=3,
数轴上表示1和-3的两点之间的距离是:|1-(-3)|=4;
②数轴上表示x和-1的两点A和B之间的距离是:|x-(-1)|=|x+1|,
如果|AB|=2,
则|x+1|=2,
∴x+1=2或x+1=-2,
解得x=1或-3.
③当代数式|x+4|+|y-7|取最小值时,
|x+4|+|y-7|=0
∴x+4=0,y-7=0,
解得x=-4,y=7,
则x-y=-4-7=-11.
故答案为:3,3,4;|x+1|,1或-3;-11.
点评 (1)此题主要考查了绝对值的含义和应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.
(2)此题还考查了数轴的特征,以及数轴上两点之间的距离的求法,要熟练掌握.

练习册系列答案
相关题目
 我校初三年级在开学初进行了跳绳测试.某班体育老师告诉该班体育委员:班上只有8%的同学得到了满分20分,要加油.体育委员将跳绳测试的统计结果绘制成如下的统计图,以便根据班级情况进行针对性训练.请你结合图中所给信息解答下列问题:
我校初三年级在开学初进行了跳绳测试.某班体育老师告诉该班体育委员:班上只有8%的同学得到了满分20分,要加油.体育委员将跳绳测试的统计结果绘制成如下的统计图,以便根据班级情况进行针对性训练.请你结合图中所给信息解答下列问题: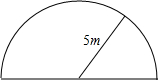 如图,某隧道是一个双向通车的隧道,隧道的截面是一个半径为5米的半圆形,一辆高4.2米,宽3米的卡车能通过该隧道吗?为什么?
如图,某隧道是一个双向通车的隧道,隧道的截面是一个半径为5米的半圆形,一辆高4.2米,宽3米的卡车能通过该隧道吗?为什么?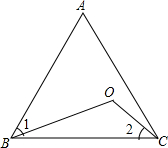 如图,O是等边三角形ABC内一点,∠1=∠2,求∠BOC的度数.
如图,O是等边三角形ABC内一点,∠1=∠2,求∠BOC的度数.