题目内容

9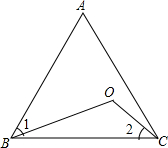．如图，O是等边三角形ABC内一点，∠1=∠2，求∠BOC的度数．

分析 根据等边三角形的性质求得∠ABC=∠1+∠OBC=60°，进而得出∠2+∠OBC=60°，然后根据三角形内角和即可求得．

解答 解：∵△ABC是等边三角形，
∴∠ABC=60°，
∴∠1+∠OBC=60°，
∵∠1=∠2，
∴∠2+∠OBC=60°，
∴∠BOC=180°-（∠2+∠OBC）=180°-60°=120°．

点评 本题考查了等边三角形每个内角都是60°的性质和三角形内角和定理，熟练掌握性质定理是解题的关键．

练习册系列答案
相关题目
19．阅读下面材料：
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为AB．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，AB=OB=|b|=|a-b|
当A、B两点都不在原点时，
①如图2，点A、B都在原点的右边|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
②如图3，点A、B都在原点的左边，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=a-b=|a-b|；
③如图4，点A、B在原点的两边，|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|；
综上，数轴上A、B两点之间的距离|AB|=|a-b|．
回答下列问题：
①数轴上表示2和5的两点之间的距离是3，数轴上表示-2和-5的两点之间的距离是3，数轴上表示1和-3的两点之间的距离是4；
②数轴上表示x和-1的两点A和B之间的距离是|x+1|，如果|AB|=2，那么x为1或-3；
③当代数式|x+4|+|y-7|取最小值时，则x-y=-11．
20．出租车的收费标准是：起步价6元，路程超过6千米的部分，每千米收费1.5元．如果某出租车行驶路程为P（P＞6）km，则司机应收费（单位：元）（1.5P-3）元．
17．（1）指出下列各小题中的两个代数式的意义有什么不同？
①5（x-3），5x-3； ②$\frac{1}{x-y}$，$\frac{1}{x}-\frac{1}{y}$．
（2）根据生活经验，试对下列各式作出解释：
 ①$\frac{1}{2}ab$；②2πx；③πR2；④$\frac{x}{41}$．
4．已知：如图，在Rt△ABC中，∠B=90°，AB=5，BC=12，AC的垂直平分线与AC，BC分别交于点D，E．求：DE的长．
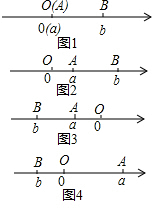
14．点A（x1，y1）和点B（x2，y2）在同一直线y=kx+b上，且k＜0，若x1＞0＞x2，则y1，y2与b的关系是（　　）
A．y1＞y2＞bB．y1＞y2＜bC．y2＞b＞y1D．y1＞b＞y
1．巴黎与北京的时差为-7小时（正数表示同一时刻比北京早的时数），如果北京时间是10月2日14时，那么巴黎时间是（　　）
A．10月2日21时B．10月2日7时C．10月2日5时D．10月1日7时
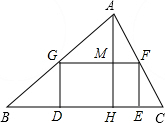18．如图，在△ABC中，矩形DEFG的一边DE在BC上，另外两个顶点G，F分别在AB，AC上，高AH交GF于M，且BC=8，AH=5，矩形DEFG的周长为12．求△AGF的面积．
19．已知：|a-1|+（ab-2）2=0．试求$\frac{1}{ab}$+$\frac{1}{（a+1）（b+1）}$+$\frac{1}{（a+2）（b+2）}$+…+$\frac{1}{（a+2004）（b+2004）}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网