题目内容
8.已知a,b(a≠b)满足a2-3a-5=0,b2-3b-5=0,则$\frac{1}{a}$+$\frac{1}{b}$=-$\frac{3}{5}$.分析 根据题意,可把a和b看作方程x2-3x-5=0的两根,根据根与系数的关系得到a+b=3,ab=-5,再变形$\frac{1}{a}$+$\frac{1}{b}$得到$\frac{a+b}{ab}$,然后利用整体代入的方法计算.
解答 解:∵a2-3a-5=0,b2-3b-5=0,
∴a和b可看作方程x2-3x-5=0的两根,
∴a+b=3,ab=-5,
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{3}{-5}$=-$\frac{3}{5}$.
故答案为-$\frac{3}{5}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
18.箱子里有黄色乒乓球和白色乒乓球各1个,它们除颜色不同外其他都完全相同,全班同学分10组作摸球试验,每组摸20次,规则为:任意摸出一球,如果是黄色,记为数字1,如果是白色,记为数字2,然后把球放回箱子里搅匀后,再重复摸一次,并记录两次摸球的数字之和,下表是记录的摸球结果.
(1)把表格中的数据补充完整;
(2)请你根据试验数据求事件“和为2”的概率;
(3)你能通过直接计算分别求得事件“和为2”、“和为3”、“和为4”的概率吗?试试看.
| 试验次数 | 20 | 40 | 60 | 80 | 100 |
| “和为2”的频数 | 6 | 8 | 14 | 24 | 27 |
| “和为2”的频率 | 0.30 | 0.20 | 0.23 | 0.30 | 0.27 |
| 试验次数 | 120 | 140 | 160 | 180 | 200 |
| “和为2”的频数 | 28 | 38 | 42 | 46 | 49 |
| “和为2”的频率 | 0.23 | 0.27 | 0.26 | 0.27 | 0.25 |
(2)请你根据试验数据求事件“和为2”的概率;
(3)你能通过直接计算分别求得事件“和为2”、“和为3”、“和为4”的概率吗?试试看.
18. 如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )
如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )
 如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )
如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
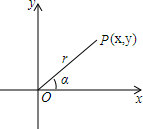 如图,在平面直角坐标系的第一象限内有一点p(x,y),点P到原点的距离OP=r,且PO与x轴的正半轴成α角.
如图,在平面直角坐标系的第一象限内有一点p(x,y),点P到原点的距离OP=r,且PO与x轴的正半轴成α角.