题目内容
14．
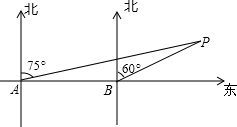某轮船由西向东航行，在A处测得小岛P的方位是北偏东75°，继续航行7海里后，在B处测得小岛P的方位是北偏东60°，则此时轮船与小岛P的距离BP=（ ）| A． | 7海里 | B． | 14海里 | C． | 3.5海里 | D． | 4海里 |
分析 先过P作AB的垂线PD，在直角△BPD中可以求得∠PAD的度数是30°，即可证明△APB是等腰三角形，即可求解．
解答 
解：过P作PD⊥AB于点D，
∵∠PBD=90°-60°=30°
且∠PBD=∠PAB+∠APB，∠PAB=90-75=15°
∴∠PAB=∠APB，
∴BP=AB=7（海里）．
故选A．
点评 此题考查的是解直角三角形的应用，解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．正确证明△APB是等腰三角形是解决本题的关键．
练习册系列答案
相关题目
9．
小丽想测量学校旗杆的高度，她在地面A点安置侧倾器，测得旗杆顶端C的仰角为α，侧倾器到旗杆底部的距离AD为10米，侧倾器的高度AB为1.5米，那么旗杆的高度CD为（ ）
小丽想测量学校旗杆的高度，她在地面A点安置侧倾器，测得旗杆顶端C的仰角为α，侧倾器到旗杆底部的距离AD为10米，侧倾器的高度AB为1.5米，那么旗杆的高度CD为（ ）| A． | （10tanα+1.5）米 | B． | （10cosα+1.5）米 | C． | （$\frac{10}{tanα}$+1.5）米 | D． | （$\frac{10}{sinα}$+1.5）米 |
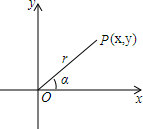如图，在平面直角坐标系的第一象限内有一点p（x，y），点P到原点的距离OP=r，且PO与x轴的正半轴成α角．