��Ŀ����
7�� ��һ���㹻���������ֽƬ������ͼ��ʾ�������ĸ���С��״һ���������Σ�Ȼ����һ���������ٰ�ͬ���ķ��������ĸ�С�����Σ����ѭ����ȥ����ͳ��ÿ�μ��������εĸ�����
��һ���㹻���������ֽƬ������ͼ��ʾ�������ĸ���С��״һ���������Σ�Ȼ����һ���������ٰ�ͬ���ķ��������ĸ�С�����Σ����ѭ����ȥ����ͳ��ÿ�μ��������εĸ�������1������ͳ�ƽ����д�±��������ݹ���д��S��n�Ĺ�ϵʽ��
| ���Ĵ�����n���� | 1 | 2 | 3 | 4 | �� | n |
| ���������n�� | �� |
��3����ԭ�����εı߳�Ϊ1����n���������������εı߳��Ƕ��٣�
���� ��1���ֱ����ó��𰸷��֣�ÿ��һ�Σ�������4�������εĻ���������3�������n�ι���4+3��n-1��=3n+1�������Σ�
��2�����ã�1���еļ��㷽������������ô𰸼��ɣ�
��3��ÿ�����α߳�����ԭ����һ�룬�ɴ˽�һ���ó��𰸼��ɣ�
��� �⣺��1��������£�
| �Ĵ�����n���� | 1 | 2 | 3 | 4 | �� | n |
| ���������n�� | 4 | 7 | 10 | 13 | �� | S=3n+1 |
���Լ���100�������Σ���Ҫ��33�Σ�
3n+1=2015�����n=671$\frac{1}{3}$��
n�������������Բ��ܽ�ԭ���������μ���2015��С�����Σ�
��3��n=1ʱ���߳�=$\frac{1}{2}$��
n=2ʱ���߳�=$\frac{1}{{2}^{2}}$��
n=3ʱ���߳�=$\frac{1}{{2}^{3}}$��
����
��n��ʱ���߳�=$\frac{1}{{2}^{n}}$��
���� ���⿼��ͼ�εı仯���ɣ��ҳ�ͼ��֮�����ϵ���ó����ֵ�������ɣ����ù��ɽ�����⣮

��ϰ��ϵ�д�
 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
�����Ŀ
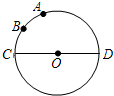 ��֪��O��ֱ��CDΪ4��$\widehat{AC}$�Ķ���Ϊ80�㣬��B��$\widehat{AC}$���е㣬��P��ֱ��CD���ƶ�����BP+AP����СֵΪ2$\sqrt{3}$��
��֪��O��ֱ��CDΪ4��$\widehat{AC}$�Ķ���Ϊ80�㣬��B��$\widehat{AC}$���е㣬��P��ֱ��CD���ƶ�����BP+AP����СֵΪ2$\sqrt{3}$��