题目内容
2.关于x的方程x2-2x+m=0有两个实数根a,b.(1)若m为正整数,求此方程的根.
(2)若y=a2-2b2-2a+4b+4.求y的取值范围.
分析 (1)表示出△,根据方程有两个实数根及m为正整数,可得m的值,继而可得方程的根.
(2)先得出m的取值范围,根据a、b是方程x2-2x+m=0的实数根,可得a2-2a+m=0,a2-2a=-m,2b2-4b+2m=0,-2b2+4b=-2m整体代入,可得y的取值范围.
解答 解:(1)∵一元二次方程x2-2x+m=0有两个实数根,
∴△=4-4m≥0,
∴m≤1,
又∵m为正整数,
∴m=1,
∴方程的根为1;
(2)∵a、b是方程x2-2x+m=0的实数根,
∴a2-2a+m=0,2b2-4b+2m=0,
∴a2-2a=-m,-2b2+4b=-2m,
∴y=a2-2b2-2a+4b+4=-3m+4,
∴y的取值范围为y≤1.
点评 本题考查了根的判别式及一元二次方程的解,解答本题的关键是掌握一元二次方程判别式与方程根的关系.

练习册系列答案
相关题目
12.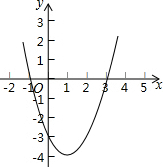 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
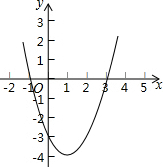 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )| A. | a>0 | |
| B. | 对称轴是直线x=1 | |
| C. | c>0 | |
| D. | 一元二次方程ax2+bx+c=0有两个不相等的实数根 |
7. 将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
(1)根据统计结果填写下表,并根据规律写出S与n的关系式:
(2)运用(1)中总结的公式计算要剪出100个正方形,共要剪几次?能不能将原来的正方形剪出2015个小正方形?为什么?
(3)若原正方形的边长为1,第n次所剪出的正方形的边长是多少?
 将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.(1)根据统计结果填写下表,并根据规律写出S与n的关系式:
| 剪的次数(n) | 1 | 2 | 3 | 4 | … | n |
| 正方形个数(n) | … |
(3)若原正方形的边长为1,第n次所剪出的正方形的边长是多少?
11.多项式-a2-1与3a2-2a+1的和为( )
| A. | 2a2-2a | B. | 4a2-2a+2 | C. | 4a2-2a-2 | D. | 2a2+2a |