题目内容
12.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,将以上三个等式两边分别相加得$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$.(1)猜想并写出:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;.
(2)直接写出下列各式的计算结果:
①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2012×2013}$=$\frac{2012}{2013}$;
②加得$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=$\frac{n}{n+1}$.
(3)探究并计算:$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2012×2014}$.
分析 (1)观察已知等式得出拆项规律,写出即可;
(2)①原式利用拆项法变形,计算即可得到结果;
②原式利用拆项法变形,计算即可得到结果;
(3)原式利用拆项法变形,计算即可得到结果.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)①原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2012}$-$\frac{1}{2013}$=1-$\frac{1}{2013}$=$\frac{2012}{2013}$;
②原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
(3)原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2012}$-$\frac{1}{2014}$)=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{2014}$)=$\frac{503}{2014}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$;(2)①$\frac{2012}{2013}$;②$\frac{n}{n+1}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7. 将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
(1)根据统计结果填写下表,并根据规律写出S与n的关系式:
(2)运用(1)中总结的公式计算要剪出100个正方形,共要剪几次?能不能将原来的正方形剪出2015个小正方形?为什么?
(3)若原正方形的边长为1,第n次所剪出的正方形的边长是多少?
 将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.(1)根据统计结果填写下表,并根据规律写出S与n的关系式:
| 剪的次数(n) | 1 | 2 | 3 | 4 | … | n |
| 正方形个数(n) | … |
(3)若原正方形的边长为1,第n次所剪出的正方形的边长是多少?
 如图,AM、AT分别为△ABC的中线及角平分线,△AMT的外接圆分别与AB、AC相交于E、F.求证:BE=CF.
如图,AM、AT分别为△ABC的中线及角平分线,△AMT的外接圆分别与AB、AC相交于E、F.求证:BE=CF.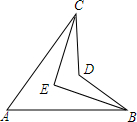 如图,∠ACD的平分线与∠ABD的平分线交于点E.试问∠A,∠CEB和∠CDB有何数量关系?为什么?
如图,∠ACD的平分线与∠ABD的平分线交于点E.试问∠A,∠CEB和∠CDB有何数量关系?为什么?