题目内容
19.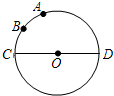 已知⊙O的直径CD为4,$\widehat{AC}$的度数为80°,点B是$\widehat{AC}$的中点,点P在直径CD上移动,则BP+AP的最小值为2$\sqrt{3}$.
已知⊙O的直径CD为4,$\widehat{AC}$的度数为80°,点B是$\widehat{AC}$的中点,点P在直径CD上移动,则BP+AP的最小值为2$\sqrt{3}$.
分析 由翻折的性质可知:PB=PB′.$\widehat{BC}=\widehat{B′C}$=40°,可求得∠B′EA=60°.当点B′、P、A在一条直线上时,PB+PA有最小值,最小值为AB′.
解答 解:过点B关于CD的对称点B′,连接AB′交CD于点P,延长AO交圆O与点E,连接B′E.
∵点B与点B′关于CD对称,
∴PB=PB′.$\widehat{BC}=\widehat{B′C}$.
∴当点B′、P、A在一条直线上时,PB+PA有最小值,最小值为AB′.
∵点B是$\widehat{AC}$的中点,
∴$\widehat{AB′}$=120°.
∴∠B′EA=60°.
∴AB′=AE•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数,求得∠B′EA=60°是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
(1)根据统计结果填写下表,并根据规律写出S与n的关系式:
(2)运用(1)中总结的公式计算要剪出100个正方形,共要剪几次?能不能将原来的正方形剪出2015个小正方形?为什么?
(3)若原正方形的边长为1,第n次所剪出的正方形的边长是多少?
 将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.
将一张足够大的正方形纸片,按如图所示虚线剪成四个大小形状一样的正方形,然后将其一个正方形再按同样的方法剪成四个小正方形,如此循环下去,并统计每次剪后正方形的个数.(1)根据统计结果填写下表,并根据规律写出S与n的关系式:
| 剪的次数(n) | 1 | 2 | 3 | 4 | … | n |
| 正方形个数(n) | … |
(3)若原正方形的边长为1,第n次所剪出的正方形的边长是多少?
11.多项式-a2-1与3a2-2a+1的和为( )
| A. | 2a2-2a | B. | 4a2-2a+2 | C. | 4a2-2a-2 | D. | 2a2+2a |