题目内容
15.将一根长为15cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是2cm≤h≤3cm.分析 根据杯子内筷子的长度取值范围得出杯子外面长度的取值范围,即可得出答案.
解答 解:∵将一根长为15cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短是等于杯子的高时为12cm,
最长时等于杯子斜边长度,即:$\sqrt{1{2}^{2}+{5}^{2}}$=13(cm),
∴h的取值范围是:(15-13)≤h≤(15-12),
即2cm≤h≤3cm.
故答案为:2cm≤h≤3cm.
点评 此题主要考查了勾股定理的应用,正确得出杯子内筷子的取值范围是解决问题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10.若分式$\frac{x-2}{x}$的值为零,则x的值是( )
| A. | 0 | B. | 2 | C. | -2 | D. | 2或-2 |
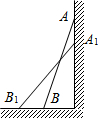 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?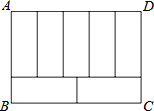 如图:周长为68的长方形ABCD被分成7个形状、大小完全一样的长方形,则ABCD的面积是多少?
如图:周长为68的长方形ABCD被分成7个形状、大小完全一样的长方形,则ABCD的面积是多少?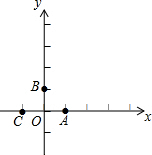 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2013的坐标为( )
如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2013的坐标为( )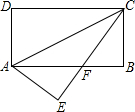 如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )
如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )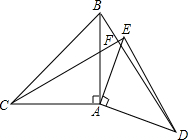 如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.
如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.