题目内容
6.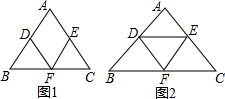 已知,△ABC中,AB=AC,点D,E,F分别是边AB,AC,BC的中点,连接DF与EF.
已知,△ABC中,AB=AC,点D,E,F分别是边AB,AC,BC的中点,连接DF与EF.(1)如图1,求证:四边形ADFE是菱形;
(2)如图2,连接DE,若AB=5cm,BC=6cm,请直接写出图中所有长为3cm的线段和四边形ADFE的面积.
分析 (1)求出AF⊥BC,根据直角三角形的性质求出AD=DF,根据三角形的中位线求出AD=EF,AE=DF,根据菱形的判定推出即可;
(2)根据三角形的中位线性质得出长为3cm的线段即可;求出△ABC的面积,求出S四边形ADFE=$\frac{1}{2}$S△ABC,即可求出答案.
解答 (1)证明:连接AF,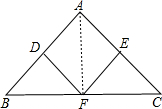
∵AB=AC,
∴AF⊥BC,
∴∠AFB=90°,
∵D为AB中点,
∴AD=BD=DF,
∵点D,E,F分别是边AB,AC,BC的中点,
∴EF=$\frac{1}{2}$AB=AD,DF=$\frac{1}{2}$AC=AE,
∴四边形ADFE是平行四边形,
∵AD=DF,
∴四边形ADFE为菱形;
(2)解:长度为3cm的线段有DE,BF,CF,
理由是:∵点D,E,F分别是边AB,AC,BC的中点,BC=6cm,
∴DE=BF=CF=$\frac{1}{2}$BC=3cm;
∵∠AFB=90°,
∴在Rt△AFB中,由勾股定理得:AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴S△ABC=$\frac{1}{2}×BC×AF$=$\frac{1}{2}×6×4$=12(cm2),
∵D为AB的中点,E为AC的中点,
∴S△AFD=S△BFD=$\frac{1}{2}$S△AFB,S△AFE=S△CFE=$\frac{1}{2}$S△AFC,
∴S四边形ADFE=S△AFD+S△AFE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×12cm2=6cm2,
即四边形ADFE的面积为6cm2.
点评 本题考查了勾股定理,三角形的中位线性质,菱形的判定的应用,能综合运用知识点进行推理和计算是解此题的关键,注意:等底等高的三角形的面积相等,有一组邻边相等的平行四边形是菱形.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案| A. | (2,-1) | B. | (-$\frac{1}{2}$,1) | C. | (-2,-1) | D. | ($\frac{1}{2}$,2) |
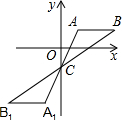 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )| A. | (-m,-n) | B. | (-m,-n-2) | C. | (-m,-n-1) | D. | (-m,-n+1) |
| A. | a<0 | B. | x=2时,y有最大值 | C. | y1y2y3<0 | D. | 5b=4c |
| A. | AB=CD,AD=BC,∠A=90° | B. | OA=OB=OC=OD | ||
| C. | AB=CD,AB∥CD,AC=BD | D. | AB=CD,AB∥CD,OA=OC,OB=OD |
 如图,在边长为6的等边△ABC中,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是3$\sqrt{3}$.
如图,在边长为6的等边△ABC中,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是3$\sqrt{3}$.